Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.2 - Ex. 6c
Considere a superfície parametrizada por
c) Essa superfície é regular?
Passo 1
Intuitivamente, uma superfície é dita “regular” quando não possui bicos. Um exemplo de superfície não regular é o cone. Veja que em seu vértice há um bico.
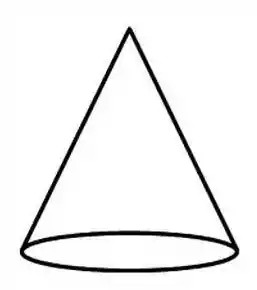
Mas como podemos saber se uma superfície é ou não regular? Podemos olhar para o seu vetor normal. Se a superfície for contínua em todos os pontos e houver pontos em que o vetor normal é nulo, então significa que ela não é regular.
Passo 2
Para a nossa superfície, temos
é contínua e de classe . Além disso, encontramos no item b) que:
Note que não há valor de e que anula ! Por exemplo, se e , então:
Se e , então:
Observação: note que não existe que anule simultaneamente e
Dessa maneira, a superfície é regular.
Resposta
Sim.
Exercícios de Livros Relacionados
Nos exercícios 8 a 14, obter uma equação cartesiana para a superfície dada. Representá-la graficamente. r → u , v = u 2 + v 2 - 1 i → + u j → + v k →
Nos exercícios 8 a 14, obter uma equação cartesiana para a superfície dada. Representá-la graficamente. r → u , v = u i → + v j → + 2 u 2 + v 2 k →
Nos exercícios 8 a 14, obter uma equação cartesiana para a superfície dada. Representá-la graficamente. r → u , v = ( u ,4 - u 2 - v 2 , v )
Nos exercícios 1 a 7, a equação dada é uma representação implícita de uma superfície S.Identifique a superfícieEscrever algumas representações explícitas de partes de S, representando-as graficamente.
Nos exercícios 8 a 14, obter uma equação cartesiana para a superfície dada. Representá-la graficamente. r → u , v = ( u ,v ,4 - u 2 - v 2 )