Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 16.Exercícios práticos - Ex. 27

Encontre parametrizações para as superfícies nos Exercícios 19-24. (Existem muitas formas de fazer isso, de modo que suas respostas podem não ser as mesmas que estão no final do livro.)

Área de um helicoide - Encontre a área da superfície do helicoide r r , θ = r cos ⁡ θ i + r sen ⁡ θ j + θ k ,     0 ≤ θ ≤ 2 π ,     0 ≤ r ≤ 1 , na figura a seguir

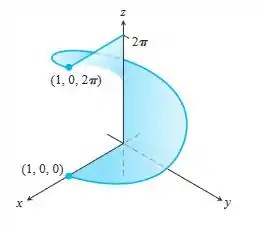
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A área da superfície parametrizada r u , v = f u , v i + g u , v j + h u , v k ,     a ≤ u ≤ b ,   c ≤ v ≤ d é dada por

A = ∬ r u × r v   d A = ∫ a b ∫ c d r u × r v   d v   d u

A seguinte superfície parametrizada no espaço é dada:

r r , θ = r cos ⁡ θ i + r sen ⁡ θ j + θ k ,     0 ≤ θ ≤ 2 π ,     0 ≤ r ≤ 1

Para encontrar a área, primeiro vamos encontrar r r   e r θ

r r = cos ⁡ θ i + sin ⁡ θ j

r θ = - r sen ⁡ θ i + r cos ⁡ θ j + k

Agora, fazendo o produto vetorial

r r × r θ = i j k cos ⁡ θ sen ⁡ θ 0 - r sen ⁡ θ r cos ⁡ θ 1 = i sen ⁡ θ - 0 - j cos ⁡ θ - 0 + k cos 2 ⁡ θ + r sen 2 ⁡ θ

Com isso,

r r × r θ = sen ⁡ θ i - cos ⁡ θ j + r k

E para o módulo

r r × r θ = sen 2 ⁡ θ + cos 2 ⁡ θ + r 2 = 1 + r 2

Passo 2

Com isso, a área da superfície é dada pela seguinte integral

A = ∫ 0 1 ∫ 0 2 π 1 + r 2   d θ   d r = ∫ 0 1 1 + r 2   θ 0 2 π   d r = 2 π ∫ 0 1 1 + r 2   d r

Substituindo os termos r = tan ⁡ u → u = arctan ⁡ r → d r = sec 2 ⁡ u   d u

∫ 1 + r 2   d r = ∫ se c 2 ⁡ u   tan 2 ⁡ u + 1   d u = ∫ sec 3 ⁡ u   d u

Aplicando a fórmula de redução com n = 3

∫ 1 + r 2   d r = sec ⁡ u tan ⁡ u 2 + 1 2 ∫ sec ⁡ d u

Desenvolvendo os termos

∫ 1 + r 2   d r = sec ⁡ u tan ⁡ u 2 + 1 2 ln ⁡ tan ⁡ u + sec ⁡ u

Portanto,

∫ 1 + r 2   d r = 1 2 r r 2 + 1 + 1 2 ln ⁡ r 2 + 1 + r

Passo 3

Finalmente, temos a seguinte situação

A = 2 π 1 2 r r 2 + 1 + 1 2 ln ⁡ r 2 + 1 + r 0 1

Desenvolvendo os termos

A = 2 π 2 2 + 1 2 ln ⁡ 2 + 1 - 0 - 1 2 ln ⁡ 1 = π 2 + ln ⁡ 2 + 1

Resposta

A = π 2 + ln ⁡ 2 + 1

Exercícios de Livros Relacionados

Encontrando o trabalho de duas formas - Encontre o trabalho realizado por F = x i + y j x 2 + y 2 3 / 2 sobre a curva plana r t = e t cos ⁡ t i + ( e t sen ⁡ t ) j entre o ponto ( 1,0 ) e o ponto ( e
Área de um triângulo - Encontre a área do triângulo no qual o plano x a + y b + z c = 1 ( a , b , c0 ) apresenta interseção com o primeiro octante. Verifique sua resposta com um cálculo vetorial aprop
Encontre parametrizações para as superfícies nos Exercícios 19-24. (Existem muitas formas de fazer isso, de modo que suas respostas podem não ser as mesmas que estão no final do livro.)Calota parabóli
Encontre parametrizações para as superfícies nos Exercícios 19-24. (Existem muitas formas de fazer isso, de modo que suas respostas podem não ser as mesmas que estão no final do livro.)Integral de sup
Encontre parametrizações para as superfícies nos Exercícios 19-24. (Existem muitas formas de fazer isso, de modo que suas respostas podem não ser as mesmas que estão no final do livro.)Faixa esférica