Exercícios de Parametrização de Curvas - Lista de Exercícios Resolvida
Questão 2
Seja a superfície de equação . Encontre uma parametrização para a intersecção de com o plano .
Ver solução completaQuestão 3
Encontre a parametrização da curva dada equação
Respeitando a inequação
Ver solução completaQuestão 5
Parametrize a curva , fronteira do triângulo de vértices , e , orientada no sentido anti-horário.
Dica: Aqui é preciso parametrizar cada um dos lados do triângulo de forma independente, afinal, cada um deles é um segmento de uma reta diferente.
Ver solução completaQuestão 6
Considere a curva parametrizada por , . O comprimento de arco entre os pontos e é igual a
(a)
(b)
(c) Nenhuma das opções
(d)
(e)
Ver solução completaQuestão 7
Determine o trabalho realizado pela força para deslocar uma partícula ao longo da elipse , no ponto , orientada no sentido anti-horário.
Ver solução completaQuestão 8
Calcule as seguintes integrais de linha ao longo do caminho indicado:
e)
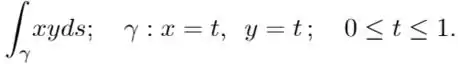
Questão 9
- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
-
Ver solução completaQuestão 10
Calcule as seguintes integrais de linha ao longo do caminho indicado:
f)
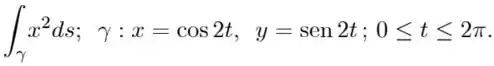
Questão 11
Parametrize a curva obtida pela interseção do cilindro com o paraboloide hiperbólico .
Ver solução completaQuestão 12
- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
- situada no primeiro octante.
Ver solução completaQuestão 13
- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
-
e , , situada no primeiro octante.
Ver solução completaQuestão 14
- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
-
, e
Ver solução completaQuestão 15
- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
- e .
Ver solução completaQuestão 16
Seja o campo vetorial . Seja a curva como a interseção do cilindro e o plano , orientada no sentido horário.
- Represente a integral de linha do campo vetorial sobre a curva através de uma integral simples definida.
- Determine o valor do campo vetorial sobre a curva .
Questão 17
Seja a curva parametrizada , .
- Qual a distância, menor possível, do ponto da curva para ao ponto da curva para ?
- Considere uma partícula de massa desprezível que percorre a curva . Qual seria a distância percorrida sobre a curva para a partícula ir do instante até o instante ?
Questão 19
Questão 4. Seja a superfície dada pela parte da esfera , calota esférica, que está acima do plano . Considere a função definida em uma região de que contém .
(a) Parametrize a superfície
Ver solução completaQuestão 21
Questão 5. Ache uma representação de parametrização das superfícies abaixo.
(a) A metade inferior do elipsoide ;
Ver solução completaQuestão 22
Considere a curva parametrizada plana
(espiral logarítmica). Observe que em coordenadas polares esta curva e descrita por
Esta curva possui auto interseções, isto é, parâmetros tais que ? Justifique sua resposta.
Mostre que o ângulo entre o vetor posição e o vetor velocidade é constante e calcule este ângulo.
Ver solução completaQuestão 23
Calcule a integral de linha , onde consiste na metade superior da circunferência de a e no segmento de reta de a
Ver solução completaQuestão 25
Considerando a superfície dada pela porção do cone limitada pelos planos e .a) Parametrize usando coordenadas polares.
Ver solução completaQuestão 26
Calcule a integral de superfície onde e é a parte do paraboloide abaixo do plano com orientação ascendente (orientada para fora da superfície).
Ver solução completaQuestão 27
1. Esboce a imagem da curva , indicando o seu sentido de percurso, sendo:
b) , .
Ver solução completaQuestão 28
1. Esboce a imagem da curva , indicando o seu sentido de percurso, sendo:
d) , .
Ver solução completaQuestão 29
2. Obter as equações paramétricas das seguintes curvas:
a) A reta que passa pelos pontos e .
Ver solução completaQuestão 30
2. Obter as equações paramétricas das seguintes curvas:
b) a curva de equação .
Ver solução completaQuestão 31
2. Obter as equações paramétricas das seguintes curvas:
c) a curva de equação .
Ver solução completaQuestão 32
2. Obter as equações paramétricas das seguintes curvas:
d) a curva de equação ; .
Ver solução completaQuestão 33
2. Obter as equações paramétricas das seguintes curvas:
e) a curva no espaço de equação ; .
Ver solução completaQuestão 34
2. Obter as equações paramétricas das seguintes curvas:
f) a curva no espaço de equação ; .
Ver solução completaQuestão 35
Calcule a integral de linha , C é o retângulo com vértices (0, 0) , (3, 0) , (3, 1) e (0, 1) por dois métodos:
- diretamente;
Questão 36
27. Seja a parte do plano limitada pelo cilindro . Uma parametrização da superfície é
a) , , com e .
b) , , , com e .
c) , , com e .
d) , , com e
Ver solução completaQuestão 37
Calcule
ao longo dos seguintes caminhos fechados, orientados positivamente:
- ao longo da elipse
Questão 38
Calcule
ao longo dos seguintes caminhos fechados, orientados positivamente:
- triângulo de vértices
Questão 42
(a) Determine a massa de um arame cujo formato é o da curva
e a densidade de massa em cada ponto é .
Ver solução completaQuestão 43
Determine a massa e o centro de massa de um arame cujo formato é o da curva
e a densidade de massa em cada ponto é .
Ver solução completaQuestão 44
Considere a reta no espaço parametrizada pela função vetorial , . Qual das seguintes equações descreve um plano que não intersecta a reta acima?
(a)
(b)
(c)
(d)
(e) Nenhuma das opções
Ver solução completaQuestão 45
(a) Identifique e faça um esboço da superfície no espaço dada por .
(b) Parametrize a curva em que é interseção das superfícies e do paraboloide hiperbólico dado por .
(c) Encontre o comprimento da curva da origem até o ponto .
Ver solução completaQuestão 46
1. Esboce a imagem da curva , indicando o seu sentido de percurso, sendo:
a) , .
Ver solução completaQuestão 47
Calcule
ao longo dos seguintes caminhos fechados, orientados positivamente:
- circunferência de centro na origem e raio 2;
Questão 48
Calcule , do ponto ao ponto , ao longo dos caminhos:
b) interseção das superfícies e .
Ver solução completaQuestão 49
Calcule , onde:
a) e é a interseção de e , percorrida no sentido anti-horário quando vista da origem.
Ver solução completaQuestão 51
3. Calcule as seguintes integrais de linha ao longo do caminho indicado:
(g) ; é o triangulo de vértices , e .
Ver solução completaQuestão 52
3. Calcule as seguintes integrais de linha ao longo do caminho indicado:
(j) ; ao longo da curva , , .
Ver solução completaQuestão 54
Calcule as seguintes integrais de linha ao longo do caminho indicado:
a)
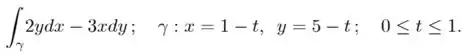
Questão 55
Calcule as seguintes integrais de linha ao longo do caminho indicado:
b)
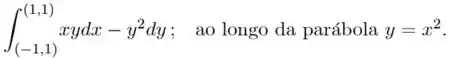
Questão 56
Calcule as seguintes integrais triplas:
a)
Em que é a região delimitada pelos planos coordenados e .
Ver solução completaQuestão 57
Calcule as seguintes integrais triplas:
b)
Em que é a região delimitada por , e .
Ver solução completa