Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 62

Encontre os pontos na curva dada onde a reta tangente é horizontal ou vertical.

r = cos ⁡ θ + s e n   θ

Passo 1

Olá, meu amigo. A gente vai resolver essa atividade juntos hoje.

O exercício fornece uma curva em coordenadas polares e pede para acharmos os pontos em que a reta tangente é horizontal ou vertical.

Para isso, primeiro devemos lembrar que

x = r cos ⁡ θ                 e                     y = r   s e n   θ

Portanto,

x = cos ⁡ θ + s e n   θ cos ⁡ θ                   e                       y = cos ⁡ θ + s e n   θ   s e n   θ

Além disso, a inclinação da tangente a nossa curva é:

d y d x = d y d θ d x d θ

Assim, a tangente será horizontal quando d y d θ = 0 e vertical quando d x d θ = 0 .

Passo 2

Vamos procurar onde a tangente é horizontal:

d y d θ = d d θ cos ⁡ θ + s e n   θ   s e n   θ

d y d θ = d d θ cos ⁡ θ sin ⁡ θ + sin 2 ⁡ θ

Utilizando a regra da cadeia e a regra do produto:

d y d θ = - s e n   θ + cos ⁡ θ   s e n   θ + cos ⁡ θ + s e n   θ cos ⁡ θ

Assim,

d y d θ = cos 2 ⁡ θ - s e n 2 θ + 2   s e n   θ cos ⁡ θ

Utilizando as identidades trigonométricas:

d y d θ = cos ⁡ 2 θ + s e n   2 θ

Portanto, a tangente horizontal acontece quando y ' θ = 0 e x ' θ ≠ 0

d y d θ = 0

0 = cos ⁡ 2 θ + sin ⁡ 2 θ

Temos então:

s e n   2 θ = - cos ⁡ 2 θ

tan ⁡ 2 θ = - 1

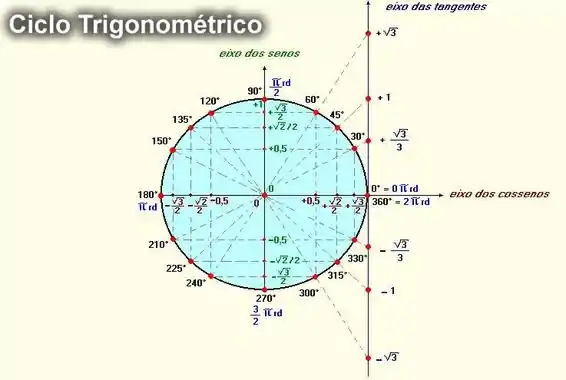
Logo, após conferimos no círculo trigonométrico das tangentes:

2 θ = 3 π 4 + n π

θ = 3 π 8 + n π 2

Na primeira volta, teremos

n = 0 ⇒ θ = 3 π 8

n = 1 ⇒ θ = 7 π 8

n = 2 ⇒ θ = 11 π 8

n = 3 ⇒ θ = 15 π 8

Passo 3

Já para os pontos de tangente vertical:

d x d θ = d d θ cos ⁡ θ + sin ⁡ θ sin ⁡ θ

d x d θ = d d θ sin ⁡ θ cos ⁡ θ + sin 2 ⁡ θ

Derivando utilizando a regra do produto e da cadeia:

d x d θ = - s e n   θ + cos ⁡ θ cos ⁡ θ - cos ⁡ θ + s e n   θ s e n   θ

Assim,

d x d θ = cos 2 ⁡ θ - s e n 2 θ - 2   s e n   θ cos ⁡ θ

d x d θ = cos ⁡ 2 θ - s e n   2 θ

Portanto,

d x d θ = 0

s e n   2 θ = cos ⁡ 2 θ

tan ⁡ 2 θ = 1

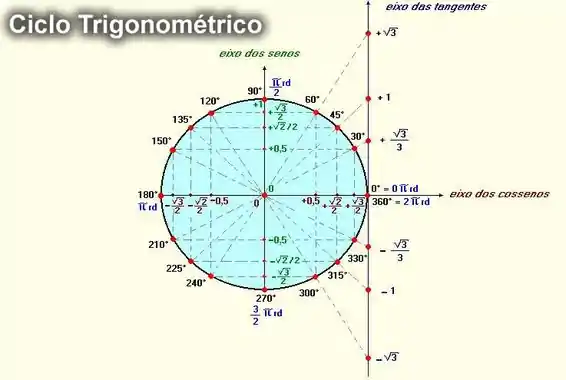
Logo, após conferimos no círculo trigonométrico das tangentes:

2 θ = π 4 + n π

θ = π 8 + n π 2

Desta forma,

n = 0 ⇒ θ = π 8

n = 1 ⇒ θ = 5 π 8

n = 2 ⇒ θ = 9 π 8

n = 3 ⇒ θ = 13 π 8

Resposta

Tangente horizontal:

θ = 3 π 8 + n π 2 ,   ��         n = 0 ,   1 ,   2 ,   3

Tangente vertical:

θ = π 8 + n π 2 ,             n = 0 ,   1 ,   2 ,   3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Elimine o parâmetro para expressar a curva na forma y = ƒ(x). a )x = 4 t 2ey = t 3 - 1 b )x = cos ⁡ tey = t gt
Encontre equações paramétricas para a curva dada.a ) R e t a p a s s a n d o p o r ( 1 , - 2 ) c o m c o e f i c i e n t e a n g u l a r 3 . b ) (x - 1)^2 + (y + 2)^2 = 9 c ) y = 4 x^2 - x d ) 9 x^2 +
Encontre equações paramétricas e um intervalo de parâmetro para o movimento de uma partícula que parta no ponto (-2, 0) no plano xy e trace o círculo x2 + y2 = 4 três vezes em sentido horário. (Existe
Encontre o valor de t g psi para a curva r = s e n^4 ((theta)/(4)) .
Mostre, por referência a uma figura, que o ângulo β entre as tangentes a duas curvas em um ponto de intersecção pode ser encontrado a partir da fórmula: t gβ = t gψ 2 - t gψ 1 1 + t g ψ 2t gψ 1 Quando