Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 65

Encontre os pontos na curva dada onde a reta tangente é horizontal ou vertical.

r = cos ⁡ 2 θ

Passo 1

Olá, meu amigo. Estarei te ajudando a resolver essa atividade hoje.

O exercício fornece uma curva em coordenadas polares e pede para acharmos os pontos em que a reta tangente é horizontal ou vertical.

Para isso, primeiro devemos lembrar que:

x = r cos ⁡ θ

y = r   s e n   θ

E a curva que iremos trabalhar é a:

r = cos ⁡ 2 θ

Portanto,

x = cos ⁡ 2 θ cos ⁡ θ

y = cos ⁡ 2 θ   s e n   θ

Além disso, a inclinação da tangente é

d y d x = d y d θ d x d θ

Assim, a tangente será horizontal quando d y d θ = 0 e vertical quando d x d θ = 0 . Então é isso, deveremos calcular as derivadas das parametrizações das nossas curvas e ao zerar, encontrar os valores de θ que queremos.

Passo 2

Vamos procurar onde a tangente é horizontal:

d y d θ = d d θ cos ⁡ 2 θ sin ⁡ θ

Aqui a gente vai utilizar a regra do produto e a regra da cadeia:

d y d θ = d d θ 2 θ ∙ d d θ cos ⁡ θ sin ⁡ θ + cos ⁡ 2 θ cos ⁡ θ

d y d θ = - 2   s e n   2 θ   s e n   θ + cos ⁡ 2 θ cos ⁡ θ

Assim, ao substituirmos a identidade trigonométrica:

sin ⁡ 2 θ = 2 sin ⁡ θ cos ⁡ θ

E

cos ⁡ 2 θ = cos 2 ⁡ θ - sin 2 ⁡ θ

d y d θ = - 2 2 sin ⁡ θ cos ⁡ θ sin ⁡ θ + cos 2 ⁡ θ - sin 2 ⁡ θ cos ⁡ θ

Então agora a gente vai realizar os produtos:

d y d θ = - 4 s e n 2 θ cos ⁡ θ + cos 3 ⁡ θ - s e n 2 θ cos ⁡ θ

Organizando os termos:

d y d θ = - 5   s e n 2 θ cos ⁡ θ + cos 3 ⁡ θ

Portanto,

d y d θ = 0

cos ⁡ θ   cos 2 ⁡ θ - 5   s e n 2 θ = 0

Logo, as situações que temos para zerar essa equação são:

cos ⁡ θ = 0

ou

cos 2 ⁡ θ = 5   s e n 2 θ

Portanto, analisando o círculo trigonométrico abaixo:

θ = π 2

θ = 3 π 2

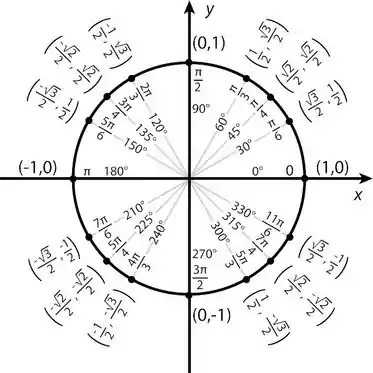
Agora para a nossa tangente:

tan ⁡ θ = ± 1 5

θ = 0.42053 + n π

θ = - 0.42053 + n π

Passo 3

Já para os pontos de tangente vertical:

d x d θ = d d θ cos ⁡ 2 θ cos ⁡ θ

Para derivar precisaremos utilizar a regra da cadeia e a regra do produto:

d x d θ = d d θ 2 θ ∙ d d θ cos ⁡ θ cos ⁡ θ + cos ⁡ 2 θ ∙ d d θ cos ⁡ θ

Organizando as derivadas:

d x d θ = - 2   s e n   2 θ cos ⁡ θ - cos ⁡ 2 θ   s e n   θ

Assim, colocando as identidades trigonométricas:

cos ⁡ 2 θ = cos 2 ⁡ θ - sin 2 ⁡ θ

sin ⁡ 2 θ = 2 sin ⁡ θ cos ⁡ θ

Realizando a multiplicação:

d x d θ = - 4   s e n   θ cos 2 ⁡ θ - s e n   θ cos 2 ⁡ θ + s e n 3 θ

Organizando:

d x d θ = s e n 3 θ - 5   s e n   θ cos 2 ⁡ θ

Portanto,

d x d θ = 0

s e n   θ   s e n 2 θ - 5 cos 2 ⁡ θ = 0

Logo, para que essa equação zere, a gente precisa de:

s e n   θ = 0

s e n 2 θ = 5 cos 2 ⁡ θ

Desta forma, olhando o círculo trigonométrico abaixo, podemos constatar:

θ = 0

θ = π

tan ⁡ θ = ± 5

θ = 1.15026 + π n

θ = - 1.15026 + π n

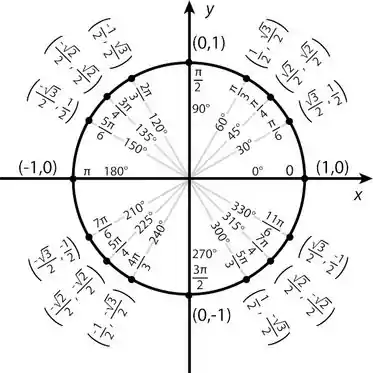
Resposta

Tangente horizontal:

θ = π 2

θ = 3 π 2

θ = 0.42053 + n π

θ = - 0.42053 + n π

Tangente vertical:

θ = 0

θ = π

θ = 1.15026 + π n

θ = - 1.15026 + π n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o ângulo no qual a cardioide r = a(1 - cos θ ) cruza o raio θ = π /2.
Encontre a centroide da região delimitada pelo eixo x e o arco da cicloide x = a t - s e nt ,y = a 1 - cos ⁡ t ,0 ≤ t ≤ 2 π
Encontre o ângulo entre o raio vetor da curva r = 2a sen 3 θ e sua tangente quando θ = π / 6 .
Desenhe a espiral hiperbólica r θ = 1. O que parece acontecer a ψ conforme a espiral gira ao redor da origem?Confirme seu achado no item (a) analiticamente.
Os círculos r = 3 cos θ e r = sen θ se intersectam no ponto 3 2 , π 3 . Mostre que suas tangentes são perpendiculares ali.