Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 10.2 - Ex. 18
Encontre os pontos na curva onde a reta tangente é horizontal ou vertical. Se você tiver uma verramenta gráfica, trace a curva.
Passo 1
Falaee, beleza?? Bom... o enunciado nos deu as seguintes equações de uma curva parametrizada:
Lembrando que a parametrização de uma curva é um processo usado para representar pontos na curva em termos de um ou mais parâmetros.
Queremos encontrar os pontos da curva onde a reta tangente é horizontal ou vertical.
Mas quando uma reta é tangente horizontal e vertical??
Bom... sabemos a reta tangente é horizontal é obtida quando:
E a reta tangente vertical é obtida quando
Então, vamos achar essas derivadas, igualar a zero para encontrar os valores de em que isso ocorre e depois substituir na parametrização da curva ( e ) para encontrar os pontos correspondentes!!
Passo 2
Vamos começar por quando a reta tangente é horizontal.
Derivando e igualando a zero, temos:
Para termos essa igualdade, temos duas possibilidades, ou:
Ou
No caso em que , temos:
E noo caso em que , temos:
Então temos uma reta tangente horizontal, quando ou quando .
Passo 3
Substituindo na parametrização da curva, temos para :
E, para :
Logo descobrimos o ponto:
Agora substituindo , temos para :
E, para :
Portanto, a reta tangente é horizontal no ponto:
Temos dois pontos nos quais as retas tangentes a curva são horizontais:
Passo 4
Agora vamos descobrir quando a reta tangente é vertical.
Assim, derivando e igualando a zero, temos:
Dividindo os dois lados por 6, nós temos a seguinte equação do segundo grau:
Resolvendo pela fórmula de Bhaskara:
Temos dois valores possíveis:
E
Passo 5
Agora vamos substituir os valores que encontramos para para encontrar os pontos onde as retas tangentes são verticais.
Substituindo na parametrização da curva, temos para :
E, para :
Assim encontramos o ponto:
Agora substituindo , temos para :
E, para :
Portanto, a reta tangente é vertical nos ponto:
Temos então dois pontos nos quais as retas tangentes a curva são verticais:
Passo 6
Bom, plotando a curva e marcando os pontos encontrados, temos:
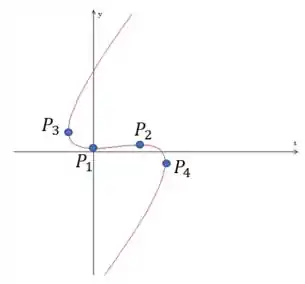
Perceba que esses pontos correspondem a retas tangentes na horizontal e vertical, veja:
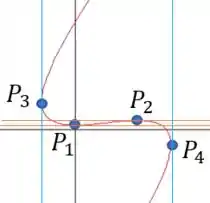
Resposta
A reta tangente é horizontal nos pontos
E vertical nos pontos