Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 17
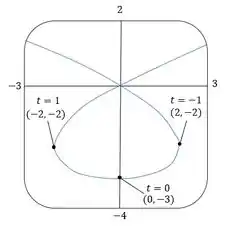
Encontre os pontos na curva onde a tangente é horizontal ou vertical. Se você tiver uma ferramenta gráfica, trace a curva.
Passo 1
Fala aí pessoal. Tranquilo? Vamos entender um pouquinho sobre o que a questão nos pede? 😊
Se liga! Temos que encontrar os pontos onde a curva tangente é vertical ou horizontal. Como vamos fazer isso?
- Vamos derivar as funções em relação a
- Vamos igualar a derivada a zero e encontrar o valor de
- Vamos substituir o valor de que encontramos nas equações originais para obter as coordenadas dos pontos na curva.
- E para finalizar, utilizaremos um software para plotar o gráfico.
Vamos começar!
Passo 2
Primeiro, vamos derivar a função, , em relação a
E
Encontramos então, para o ponto vertical.
Passo 3
E derivando a função , ficamos com:
Igualando a zero
Simplificando função
Para o ponto horizontal encontramos ou .
Passo 4
Perceba que encontramos três valores para , agora vamos encontrar pontos substituindo nas equações de e .
Para
Sendo assim, o ponto vertical será:
Passo 5
Para
Sendo assim, o ponto horizontal será:
Passo 6
Para
Sendo assim, o segundo ponto horizontal será:
Passo 7
A curva tem uma horizontal tangente em e tangentes verticais em e .
E a curva fica da seguinte maneira:
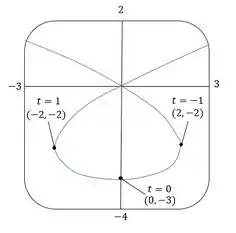
Resposta
A curva tem uma horizontal tangente em e tangentes verticais em e .
