Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.9 - Ex. 11

Encontre a primitiva mais geral da função. (Verifique sua resposta derivando.)

f x = 10 x 9

Passo 1

Eaee, belezinha???

Bom galera, nessa questão estamos interessados em encontrar a primitiva da função f :

f x = 10 x 9

Para isso, iremos utilizar a seguinte tabelinha:

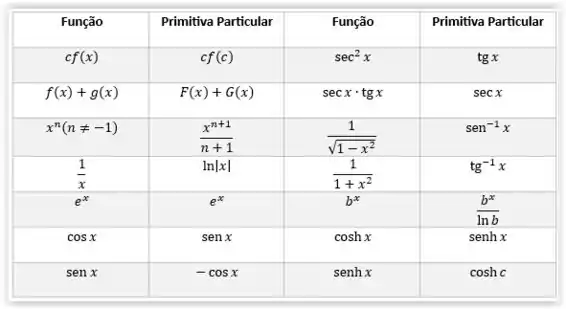
Passo 2

Para encontrar a primitiva de f , iremos utilizar a Regra da Potência, que é

x n = x n + 1 n + 1   p a r a   n ≠ - 1

Para ficar melhor a nossa expressão, a gente deixa ela assim:

f x = 10 x - 9

Passo 3

Aplicando a Regra da Potência em f , temos que a primitiva é dada por:

F x = 10 * x - 9 + 1 - 9 + 1 ∴

(lembre-se que o 10 é constante)

F x = 10 * x - 8 - 8 ∴

F x = - 5 4 x 8

Passo 4

Para conferir podemos derivar F ( x ) , lembra como a divisão é o inverso da multiplicação? Para derivadas e primitivas/integrais funciona da mesma forma. Vamos usar a regra da potencia das derivadas, lembra dela?

f x = x n → f ' x = n x n - 1

Aplicando, temos:

F ' x = - 5 4 x - 8 ' ∴

F ' x = - 5 4 - 8 x - 8 - 1 ∴

F ' x = 40 4 x - 9 ∴

F ' x = 10 x 9

E temos a mesma função que tínhamos no começo!

F ' x = f ( x )

Então F ( x ) é a primitiva de f ( x ) .

Resposta

F x = - 5 4 x 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

d) (d y)/(d x) = (1)/(1 + x^2) e y (0) = 0
Uma partícula desloca-se sobre o eixo x com função de posição x = x t ,t ≥ 0 . Determine x = x t , sabendo que d )d x d t = 1 1 + t 2ex 0 = 0
Uma partícula desloca-se sobre o eixo x com função de posição x = x t ,t ≥ 0 . Determine x = x t , sabendo que e )d 2 x d t 2 = cos ⁡ 2 t ,v 0 = 1ex 0 = 0
Uma partícula desloca-se sobre o eixo x com função de posição x = x t ,t ≥ 0 . Determine x = x t , sabendo que d )d 2 x d t 2 = e - t ,v 0 = 0ex 0 = 1
Esboce o gráfico da função y = y (x) , x in R , Sabendo quea ) (d y)/(d x) = 2 x - 1 e y (0) = 0