Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.2 - Ex. 11d
d) e
Passo 1
Vamos lá resolver essa questão!
Temos que a primitiva nada mais é que a função que derivamos e chegamos a função mostrada no enunciado. Então beleza, mas qual função que nós derivamos para chegar em ? Vamos lá!
Temos:
Se queremos saber a função , teremos que:
Passo 2
Ao olhar para a função , devemos pensar em uma função que foi derivada e seu resultado foi esse, essa função que foi derivada será a nossa primitiva. Note que, ao derivarmos a função inversa da tangente, teremos:
No capítulo 8, podemos ver mais detalhadamente a resolução por partes dessa derivada, dá uma olhadinha la 😉.
Passo 3
Beleza, agora sabemos a função que foi derivada, e ela será a nossa primitiva, porémmmm, carrega consigo uma constante qualquer, observe:
Temos que , logo:
Temos que , daí:
Passo 4
Plotando o gráfico da nossa função , teremos:
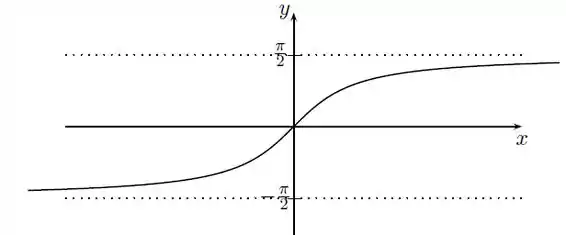
Resposta
A nossa função é .