Esboce o gráfico da função Sabendo que
Passo 1
Se temos:
Podemos dizer que:
Passo 2
Agora que achamos uma maneira de encontrar vamos fazer a integral e achar a função:
Se quisermos vamos substituir na equação:
Como o exercício disse que , então podemos igualar os valores de e achar o valor de k:
Então:
Passo 3
Agora que temos a função precisamos do gráfico
Para equação de segundo grau precisamos de alguns dados. O primeiro é se , pro nosso caso ;
O segundo são os valores em que , calculamos assim:
E podemos usar a integral pra achar os valores de mínimo do gráfico:
Vamos na equação e substituímos esse por e achamos o mínimo também:
Então agora temos os pontos em que , o ponto de mínimo e o lado da concavidade, assim o desenho fica:
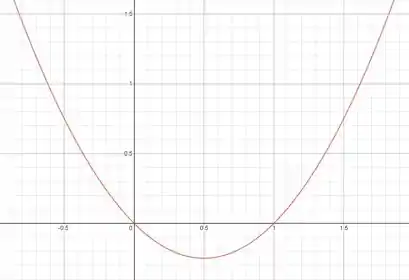
Resposta
