Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.9 - Ex. 24
Encontre uma representação em série de potências para , trace e várias somas parciais na mesma tela. O que acontece quando aumenta?
24.
Passo 1
Beleza, galera?
Como pede a questão, vamos representar em uma série de potências, fazer o gráfico e as somas parciais, principalmente analisar quando aumentar.
Olha bem pra nossa função, podemos reescrevê-la como uma integral:
Mas sabemos que a expressão dentro da integral corresponde à soma de uma série geométrica de primeiro termo e razão . A série geométrica tem essa cara aqui:
E a gente precisa representar da mesma forma. Assim, teremos
Organizando, para que fique bem parecida com a fórmula da série geométrica:
Agora integrando, somamos em :
onde é uma constante de integração.
Passo 2
Agora, se usarmos a função original e fizermos , descobriremos o valor da constante :
Então,
Passo 3
Show! Agora vamos traçar e várias somas parciais a partir da série de potências encontrada no passo anterior:
Graficamente falando, teremos
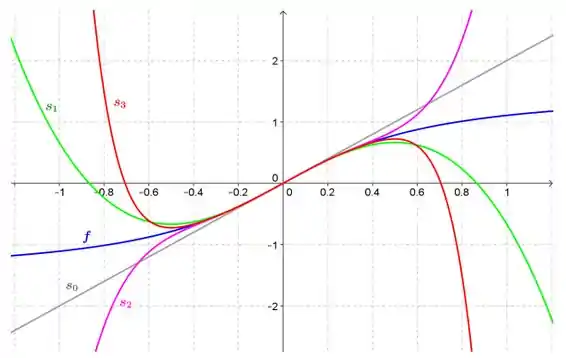
Perceba que, à medida que aumenta, as somas parciais se aproximam cada vez mais de no intervalo de convergência, ou seja, quando .