Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 18
Encontre e esboce o domínio da função.
Passo 1
Eaee, tudo tranquilinho?? Bom... o enunciado nos deu a seguinte função de duas variáveis:
Queremos determinar o domínio de , ou seja, queremos saber que valores de e que podem ser usados para que seja real.
Para definir o domínio é melhor olhar para as retrições que possibilitam que a gente tenha uma solução real.
Em seguida, a gente vai plotar o nosso domínio!! 😉
Passo 2
Temos que:
Observe que temos duas retrições aqui (uma para o logaritmo e outra no denominador):
Sabemos que o argumento do logaritmo deve ser maior que zero, ou seja:
Isso implica que:
E,por outro lado, o denominador deve ser diferente de zero, ou seja:
Isso implica que:
Multiplicando tudo por :
(não esquece que a desigualdade é invertida)
Passo 3
Logo, o domínio é definido por:
Note que o domínio está dentro de um circunferência de raio :
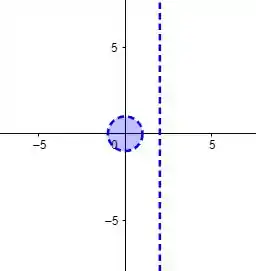
Observação: a reta tracejada é uma característica da primeira restrição que descobrimos .
Resposta
