Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 46
Encontre a série de Maclaurin de (através de qualquer método) e o seu raio de convergência. Faça o gráfico de e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a relação entre esses polinômios e ?
Passo 1
Nesse exercício iremos analisar a função:
Com o auxílio da Tabela 1, temos que:
Passo 2
Dessa forma:
Passo 3
A série para converge para , logo, seu raio de convergência é . Dessa forma, a série para também possui um raio de convergência:
O gráfico que compara e os primeiros polinômios de Taylor é mostrado a seguir:
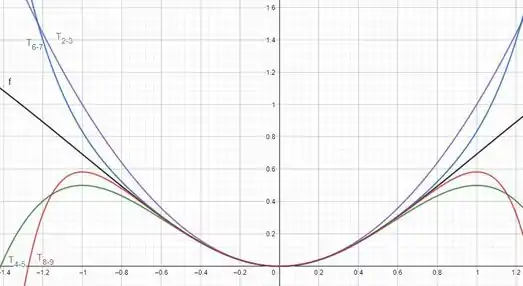
Através do gráfico é possível notar que se aproxima de próximo de zero conforme aumenta.
Resposta
Através do gráfico é possível notar que se aproxima de próximo de zero conforme aumenta.
Exercícios de Livros Relacionados
Use séries para aproximar a integral definida com a precisão indicada. ∫ 0 0 , 5 x 2 e - x 2d x e r r o0,001
Use séries para aproximar a integral definida com a precisão indicada. ∫ 0 0,2 tg - 1 ( x 3 ) + sen ( x 3 ) d x (cinco casas decimais)
Use multiplicação ou divisão de séries de potências para encontrar os três primeiros termos diferentes de zero na série de Maclaurin de cada função. y = x sen x
Encontre a soma da série. 1 - ln 2 + ln 2 2 2 ! - ln 2 3 3 ! + …
Mostre que a função definida por não é igual à sua série de Maclaurin.Trace a função na parte (a) e comente seu comportamento próximo a origem.