Encontre a série de Maclaurin de (através de qualquer método) e o seu raio de convergência. Faça o gráfico de e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a relação entre esses polinômios e ?

Substituindo por , obtemos a série para

Ao multiplicar pela série de , obtemos a série para . No entanto, é importante notar que a potência de é após a multiplicação.

Portanto, a série resultante para é:

E, reescrevendo essa série, podemos ver que o primeiro termo, , é substituído por após a multiplicação por . Portanto, começamos a nova série com .

Para manter a ordem dos termos, vamos ajustar o índice da soma de para .

Quando ajustamos o índice de soma, a fórmula Surge porque, ao iniciar a soma de , queremos que o primeiro termo corresponda a , que é . Para manter essa correspondência, substituímos por no denominador , o que nos dá

Portanto, a série reescrita para é:

Como a série para converge para todo x, o mesmo acontece para a série de . Assim, seu raio de convergência é:

O gráfico que compara e os primeiros polinômios de Taylor é mostrado a seguir:

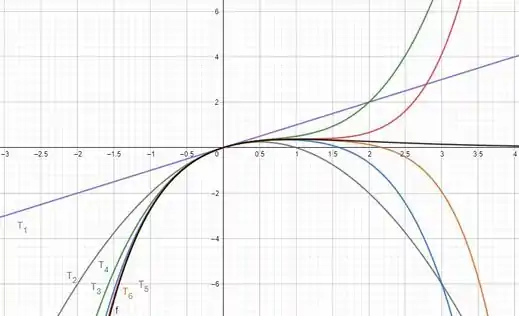
Através do gráfico é possível notar que se aproxima de próximo de zero conforme aumenta.