Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 45
Encontre a série de Maclaurin de (através de qualquer método) e o seu raio de convergência. Faça o gráfico de e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a relação entre esses polinômios e ?
Passo 1
E aí, galerinha! Tudo tranquilo?
A questão quer que a gente encontre a série de Maclaurin de :
Achar a série de Maclaurin de uma função é expressá-la como uma soma infinita de termos (série) calculados a partir de suas derivadas em um ponto, que aqui para as séries de Maclaurin é . A série de Maclaurin nada mais é que a série de Taylor com e é assim:
Olhando nosso formato de série vemos que o que falta encontrarmos é justamente que são as derivadas de no ponto zero vezes. Encontrando esse termo, nós substituímos em e temos nossa série de Maclaurin pra função que o enunciado pede.
Acontece que geralmente precisamos ter esse trabalho todo com séries de Taylor centradas em outros valores de . Para , temos as séries de Maclaurin e já temos essas séries tabeladas e prontas na teoria do nosso livro, inclusive com seus raios de convergência .
O Raio de convergência da série de Maclaurin para , é
ou seja, a série converge para qualquer valor de .
Por fim a questão pede para traçarmos os polinômios de Taylor da série, que nada mais são que os próprios termos da série, que são do formato de polinômios de .
Traçamos esses polinômios e a nossa função e observamos o comportamento dessas curvas.
Bora?
Passo 2
Olhando na nossa teoria (Tabela 1 da sessão 11.10), sabemos que a série de Maclaurin para é:
Dessa forma, como queremos a mesma série, mas para é só mudarmos o argumento de para :
E os termos da série assumem os valores:
Passo 3
O enunciado pede para traçarmos e os primeiros polinômios de Taylor () que são nada mais que você pegar a série somente até um certo termo, então os primeiros polinômios são
E assim podemos continuar até onde quisermos. O gráfico que compara e os primeiros polinômios de Taylor é mostrado a seguir:
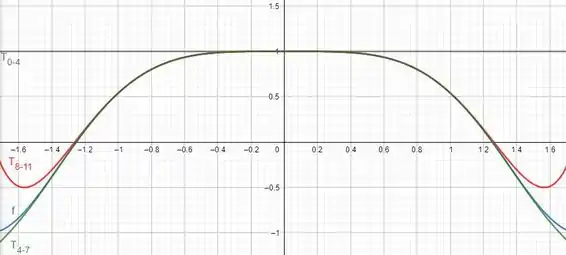
Através do gráfico é possível notar que se aproxima de próximo de zero conforme aumenta.
Resposta
Através do gráfico é possível notar que se aproxima de próximo de zero conforme aumenta.