Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 48
Encontre a série de Maclaurin de (através de qualquer método) e o seu raio de convergência. Faça o gráfico de e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a relação entre esses polinômios e ?
48.
Passo 1
Fala galera! Tudo beleza?
Então, a questão nos deu uma função e pede uma série de Maclaurin pra ela, além do raio de convergência, seu gráfico e os primeiros polinômios de Taylor.
A gente tá analisando a função
Com o auxílio da Tabela 1, que aparece nessa seção, temos que:
Passo 2
Sendo assim, podemos substituir por . Assim, ó:
Show, né?
E substituindo por , chegamos a essa outra representação aqui:
Passo 3
Pra gente descobrir o raio de convergência, basta jogarmos na fórmula do Teste da Razão:
Onde e
Pela divisão de frações, invertemos o denominador multiplicando-o:
Podemos cancelar alguns termos e simplificar alguns:
Para que o limite não seja indeterminado, iremos deixar em evidência:
Como , logo:
Com isso, seu raio de convergência é .
Passo 4
O gráfico que compara e os primeiros polinômios de Taylor, que já descobrimos é mostrado a seguir:
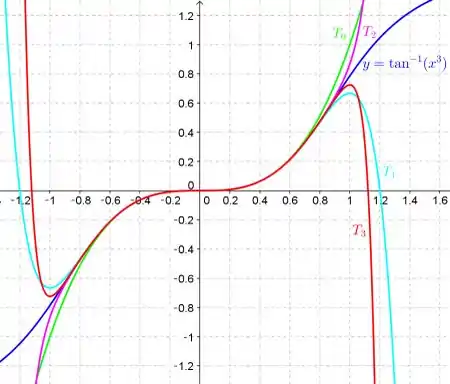
Através do gráfico é possível notar que se aproxima de próximo de zero conforme aumenta.
Resposta
Através do gráfico é possível notar que se aproxima de próximo de zero conforme aumenta.