Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 27
Use o Teorema da Estimativa de Séries Alternadas ou a Desigualdade de Taylor para estimar a gama de valores de para os quais a aproximação dada tem precisão dentro do erro estabelecido. Verifique sua resposta graficamente.
Passo 1
Fala galera, nesse exercício apesar de termos apenas dois termos a série parece ser do tipo alternada, logo a melhor opção é usar o Teorema da Estimativa de Séries Alternadas, que é um teorema mais específico para esse tipo de série , acaba sendo mais direto e simples .
Relembrando o que diz o Teorema:
Então
Função que queremos aproximar.
: Soma dos primeiros termos da série de Taylor de
: Coeficiente do termo -ésimo na expansão de Taylor.
: Erro ou resto da série de Taylor, que quantifica a diferença entre a função original
e sua aproximação .
Mas o que isso quer dizer?
Se tivermos uma série alternada, o erro de uma estimativa é menor que o próximo termo da série em módulo, porque desconsidera o sinal de .
Então o que iremos fazer é achar quem é o próximo do termo da série e compará-lo com o erro que queremos obter. Vamos lá??
Passo 2
Se dermos uma olhada na série que os enunciado nos dá, ela é bem semelhante com a série de Maclaurin do :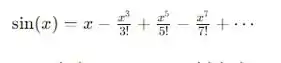 
Nós temos que :
Que pode se escrito como :
Lembra que no passo anterior vimos que precisávamos encontrar o próximo termo??
Olhando para as duas séries podemos afirmar que o próximo termo será
Beleza, agora o nosso erro precisa ser menor que esse termo que achamos. Podemos escrever isso de acordo com a fórmula:
Lembrando que
Passo 3
Se queremos um erro menor que , podemos dizer que
Isolando o
Passo 4
Agora podemos plotar esse gráfico em um software como o WolframAlpha ou até mesmo o chat gpt . Vai ficar assim:
Temos em vermelho o polinômio e em preto e , que são as margens de erro aceitáveis e o polinômio encontra o limite em , então os valores da nossa estimativa estão dentro da margem de erro.
Como a função é simétrica, o limite inferior do intervalo vai ser