Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.10 - Ex. 33

Encontre a série de Maclaurin f (por qualquer método), e seu raio de convergência. Plote f e seus primeiros polinômios na mesma tela. O que você observa sobre a relação entre esses polinômios e f ?

f x = 1 + x

Passo 1

Fala galera, tudo bem?

Essa questão pede várias coisas, então vamos ver com calma:

  1. Encontrar a série de Maclaurin (que é nada mais que a série de Taylor centrada no 0 ) pra essa função que ela da.

    2. Pra isso, a gente vai usar a definição de série de Maclaurin:

    f x = ∑ n = 0 ∞ f n 0 n ! x n

    Depois, vamos calcular as derivadas da função no ponto 0 , generalizar uma fórmula para f n 0 , e substituir na expressão da série de Maclaurin.

  2. Encontrar o raio de convergência da série, que determina o intervalo em torno de 0 onde a série converge. Pra encontrar, vamos usar o Teste da Razão (ou Teste da Raíz, dependendo de como for a série)

  3. Plotar o gráfico de f e seus primeiros polinômios, ou seja, o gráfico da função f e a série finita de Maclaurin:

f x ≈ ∑ n = 0 k f n 0 n ! x n

Para alguns valores pequenos de k ( k = 1 ,   2 ,   3 ,   4 … )

E por último avaliar o que a gente consegue observar dessa relação dos gráficos que plotamos.

Então vamos fazer passo a passo!

Passo 2

Começamos calculando as derivadas da função f , no ponto x = 0 e tentando identificar o padrão delas!

f 0 = 1

f ' x = 1 2 ⋅ 1 + x - 1 2 ⟹ f ' 0 = 1 2

f ' ' x = - 1 4 ⋅ 1 + x - 3 2 ⟹ f ' ' 0 = - 1 4

f 3 ( x ) = 3 8 ⋅ 1 + x - 5 2 ⟹ f 3 0 = 3 8

f 4 x = - 15 16 ⋅ 1 + x - 7 2 ⟹ f 4 0 = - 15 16

Vamos achar o padrão:

- Como as derivadas de ordem par têm sinal negativo, e as de ordem ímpar têm sinal positivo, vai aparecer um termo - 1 n - 1

- Os numeradores são produtos dos números ímpares ( 1 ; 3 = 1 ∙ 3 ; 15 = 1 ∙ 3 ∙ 5 ). O número que esse produto para é ( 2 n - 3 ) , ou seja, podemos expressar o numerador como 1 ∙ 3 ∙ 5 ∙ … ∙ ( 2 n - 3 ) , para n ≥ 2

- Os denominadores são potências de 2 , expressas por 2 n

Usando isso, a gente pode generalizar a derivada de ordem n como:

f n 0 = - 1 n - 1 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ ( 2 n - 3 ) 2 n ,   p a r a   n ≥ 2

Portanto, a função é escrita através da série de Maclaurin por:

f x = ∑ n = 0 ∞ f n 0 n ! x n

f x = f 0 + f ' 0 ∙ x + ∑ n = 2 ∞ f n 0 n ! x n

f x = 1 + x = 1 + x 2 + ∑ n = 2 ∞ - 1 n - 1 ⋅ 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ ( 2 n - 3 ) 2 n ⋅ n ! x n

Passo 3

Para determinarmos o raio de convergência, vamos utilizar o Teste da Razão. Pra isso, calculamos

L = lim n → ∞ ⁡ a n + 1 a n

E consideramos que a série converge quando L < 1 .

Vamos começar calculando a n e a n + 1 :

a n = - 1 n - 1 ⋅ 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2 n - 3 2 n ⋅ n ! x n

a n + 1 = - 1 n ⋅ 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2 n - 3 ∙ ( 2 n - 1 ) 2 n + 1 ⋅ n + 1 ! x n + 1

Portanto,

a n + 1 a n = - 1 n 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2 n - 3 2 n - 1 ⋅ x n + 1 2 n + 1 ⋅ n + 1 ! ⋅ 2 n ⋅ n ! - 1 n - 1 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2 n - 3 ⋅ x n

Simplificando:

= - 1 n - 1 n - 1 ∙ 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2 n - 3 2 n - 1 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2 n - 3 ∙ x n + 1 x n ⋅ 2 n 2 n + 1 ∙ n ! n + 1 ! =

= - 1 ⋅ 2 n - 1 ∙ x ∙ 1 2 ∙ 1 n + 1

Portanto:

a n + 1 a n = - 1 ⋅ 2 n - 1 2 n + 2 ∙ x

= - 1 ∙ 2 n - 1 2 n + 2 ∙ x

Calculando o limite quando n → ∞ , temos

L = lim n → ∞ ⁡ 2 n - 1 2 n + 2 ∙ x = x

Como a série converge para L = x < 1 , o raio de convergência é R = 1 .

Passo 4

Só nos falta obter o plot da nossa função f e das primeiras aproximações:

f x = 1 + x

T 1 ( x ) = 1 + x 2

T k x = 1 + x 2 + ∑ n = 2 k - 1 n - 1 ⋅ 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ 2 n - 3 2 n ⋅ n ! x n , p a r a   k ≥ 2

Para isto, vamos utilizar softwares que nos ajudem no esboço!

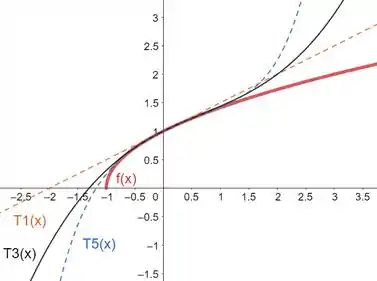
Pode-se observar que à medida em que aumentamos a ordem do polinômio, a função se aproxima cada vez mais da curva f x = 1 + x , para valores próximos de x = 0 .

Resposta

f x = 1 + x 2 + ∑ n = 2 ∞ - 1 n - 1 ⋅ 1 ⋅ 3 ⋅ 5 ⋅ … ⋅ ( 2 n - 3 ) 2 n ⋅ n ! x n

Raio de convergência igual a 1.

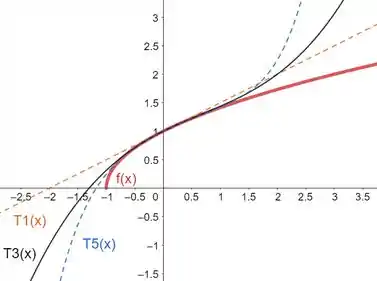
À medida em que aumentamos a ordem do polinômio, a função se aproxima cada vez mais da curva f x = 1 + x , para valores próximos de x = 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 9 a 16, determine a série de Taylor da função em torno do ponto x 0 . Determine também, o raio de convergência da série.13. ln ⁡ x , x 0 = 1
Encontre a série de Maclaurin f ( x ) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que R n → 0 .] Também encontre o raio de converg
Use a série de Maclaurin para e x para calcular 1 / e 10 com precisão de cinco casas decimais.
Use a série binomial para expandir 1 / 1 - x 2 Use a parte (a) para encontrar a série de Maclaurin de sen - 1 ⁡ x .
Expanda 1 / 1 + x 4 como uma série de potências.Utilize a parte (a) para estimar 1 / 1 , 1 4 com precisão de três casas decimais.