Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.9 - Ex. 19
Encontre uma série de potências para , plote e varias somas parciais na mesma tela. O que acontece quando aumenta?
Passo 1
Eai turminha, tudo bem com vocês!? Espero que sim! Bora responder mais uma!
Vamos compreender o enunciado primeiro, certo? Temos uma função da qual precisamos encontrar uma série de potências, e também plotar f e varias somas parciais no mesmo gráfico.
Como vamos resolver essa questão?
Vamos pensar juntos um pouco. Observe que para a função não temos nenhuma serie de potência. Mas já pensou que podemos enxergar a derivada dessa função, como iria ficar? Fazendo alguns ajustes, ela vai ficar parecida com uma função que conhecemos, a série geométrica:
Sabendo disso, obtemos a série de potência. Mas lembre-se, encontramos a série de potência para a derivada, logo precisamos aplicar a integral na série, para termos . Já para fazer o gráfico, podemos expandir a série, e para cada assumimos uma nova função.
Bora lá fazer essas etapas!
Passo 2
Para obtermos a função como uma série de potências, vamos avaliar sua derivada:
Observe a expressão que encontramos, muita parecida com a soma da série geométrica né?
Vamos fazer mais algumas manipulações, colocando em evidência no denominador:
Percebam que agora temos um termo conhecido, do qual sabemos a s��rie de potência. Ele pode ser escrito por:
Portanto, temos que:
Passo 3
Bom, encontramos uma série de potência para .
Mas lembre-se, que queremos saber a série de potência para f(x), para isso, vamos integrar ambos os lados:
Resolvendo esta integral, temos:
Percebam uma coisa. Todo o trabalho que tivemos até aqui, foi tentar transformar todo o somatório em alguma série (compactar a resposta).
Além disto, muito cuidado nesta hora. Não podemos esquecer da constante de integração! Precisamos descobrir qual o valor de . Como fazemos isso?
Para isto, basta fazermos na equação acima. Logo,
Portanto, a representação da função em série de potência é:
OBS: Percebam que a função converge em (não testamos as extremidades). É importante sabermos disto para podermos resolver o próximo passo e inclusive obter o valor de C na nossa série.
Passo 4
Já conhecemos a série de potência, certo?
Agora, precisamos obter um gráfico que mostre algumas somas parciais da nossa série. Para isto, vamos precisar do auxílio de softwares. Vejamos então abaixo:
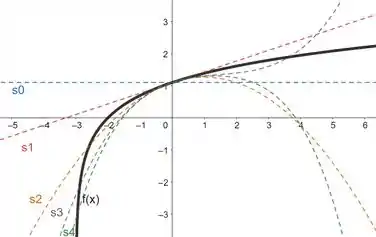
Percebam que à medida em que aumentamos a ordem da soma parcial, ou seja, conforme aumenta a nossa função se aproxima cada vez mais da função .
Resposta
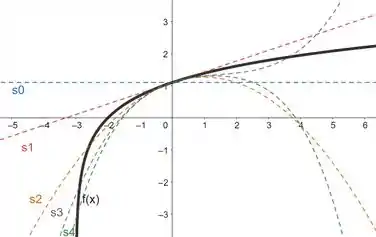
À medida em que aumentamos o valor de , nos aproximamos mais de .