Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.9 - Ex. 22
Encontre uma representação em série de potências para , o gráfico de e várias somas parciais no mesmo gráfico. O que acontece com o incremento de ?
Passo 1
Nesse exercício iremos analisar a seguinte função:
De acordo com o exemplo 6 apresentado nessa mesma seção no livro, podemos reescrever a função como:
Passo 2
Essa série é convergente para:
Sendo assim, o raio de convergência é:
Passo 3
As somas parciais da série são:
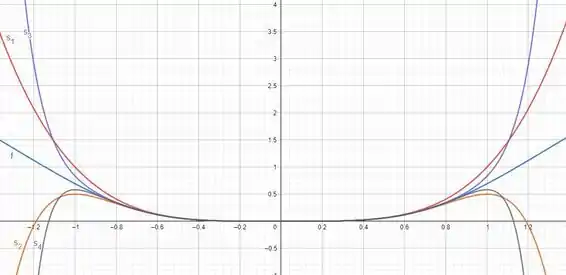
É possível perceber que, com o incremento de , se aproxima do intervalo de convergência encontrado no passo 2, . O gráfico contendo o gráfico de e as primeiras somas parciais é mostrado a seguir:
Resposta
Exercícios de Livros Relacionados
Encontre uma representação em série de potências para f , trace f e várias somas parciais s n x na mesma tela. O que acontece quando n aumenta? f x = x x 2 + 16
Calcule a integral indefinida como uma série de potências. Qual é o raio de convergência? ∫ t 1 - t 8 d t
Encontre uma representação em série de potências para a função e determine o raio de convergência. f x = a r c t g x 3
Encontre uma representação em série de potências para f , trace f e várias somas parciais s n x na mesma tela. O que acontece quando n aumenta? f x = ln ( x 2 + 4 )
Encontre uma representação em série de potências para a função e determine o raio de convergência. f x = x 3 x - 2 2