Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.9 - Ex. 21
Encontre uma representação em série de potências para , faça o gráfico de e de várias somas parciais no mesmo gráfico. O que acontece com o incremento de ?
Passo 1
Vamos lá meu amigo! Esse exercício que você encontre uma série de potência que seja equivalente a função dada. Para isso iremos utilizar o padrão das séries geométricas:
Ou seja, iremos manipular nossa série para escrever algo parecido com isso. Após isso, iremos criar o gráfico da função e das somas parciais da série. Após isso iremos comparar os gráficos e então responder o que acontece com a soma com o incremente de .
Passo 2
Nesse exercício iremos analisar a seguinte função:
Podemos reescrever a função como:
Porém, precisamos que no denominador seja uma subtração para podermos utilizar a definição da série geométrica.
Então:
Agora sim né: Vamos fazer uma substituição ode variáveis;
De modo que:
Ou seja:
Passo 3
Séries geométricas convergem quando:
Por definição:
Em que: se a série é convergente.
Então essa série é convergente para:
Sendo assim, o raio de convergência é:
E, reescrevendo como uma série de potência, temos:
Passo 4
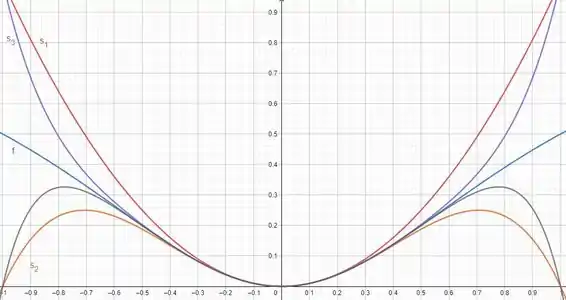
As somas parciais da série são:
Então os termos são:
É possível perceber que, com o incremento de , se aproxima do intervalo de convergência encontrado no passo 2, . O gráfico contendo o gráfico de e as primeiras somas parciais é mostrado a seguir:
