Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.9 - Ex. 20
Encontre uma série de potências para , plote e varias somas parciais na mesma tela. O que acontece quando aumenta?
Passo 1
Faaaaala galerinha, tudo na paz!? Vamos gabaritar mais uma!
Bora lá comigo! Primeiro vamos focar em entender o enunciado, certo?
Temos uma função da qual precisamos encontrar uma série de potência, e também plotar no mesmo gráfico a função e algumas somas parciais da série.
E agora? Como começo essa questão?
Primeiro observe a função fornecida. Você concorda que ela nos lembra uma função conhecida, a série geométrica. Onde é a razão:
Repare, que se fizermos algumas modificações em podemos escrevê-la como esse somatório acima. Posterior, podemos fazer o gráfico expandindo a série, ou seja, assumindo uma nova função para cada .
Vamos lá fazer essas etapas!
Passo 2
Conforme comentamos antes, vamos deixar a função com a cara da série geométrica. Vejamos então:
Foquem na expressão que temos dentro dos parênteses. Repare como ficou a cara da série geométrica:
Agora, conseguimos escrever como serie.
Vamos ter:
Manipulando um pouco a expressão:
Portanto, a nossa função, em série de potências é:
Passo 3
Agora, vamos obter o gráfico!
Precisamos obter um gráfico que mostre algumas somas parciais da nossa série. Para isto, vamos precisar do auxílio de softwares. Vejamos então abaixo:
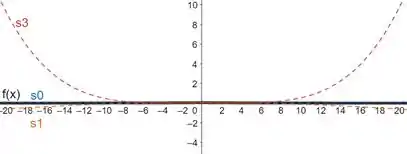
À medida em que aumentamos o valor das somas parciais, a nossa função fica cada vez mais próxima da função dentro do intervalo de convergência.
Resposta
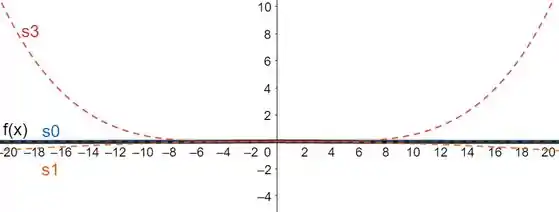
À medida em que aumentamos o valor das somas parciais, a nossa função fica cada vez mais próxima da função dentro do intervalo de convergência.