Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.5 - Ex. 12

  1. Encontre a solução do problema de valor inicial dado.
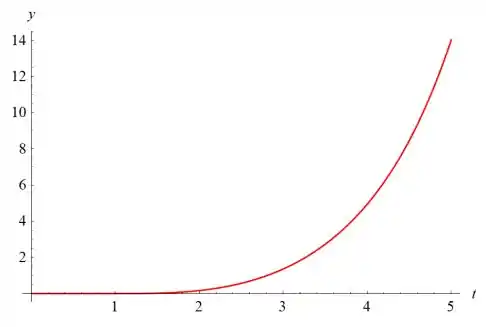
  2. Desenhe um gráfico da solução.

y ( 4 ) - y = δ t - 1 ;     y 0 = 0 ,   y ' 0 = 0 ,   y ' ' ( 0 ) = 0 ,   y ' ' ' ( 0 ) = 0 .

Passo 1

Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:

Y ( s )   =   L { y t } = ∫ 0 ∞ y t   e - s t   d t

Consequentemente, as derivadas se transformam da seguinte maneira.

L y ' t = s Y s - y 0

L y ' ' t = s 2 Y s - s y 0 - y ' 0

L y ' ' ' t = s 3 Y s - s 2 y 0 - s y ' 0 - y ' ' 0

L y 4 t = s 4 Y s - s 3 y 0 - s 2 y ' ' 0 - s y ' ' 0 - y ' ' ' 0

Aplique a conversão Laplace nos dois lados da EDO:

L y ( 4 ) - y = L { δ t - 1 }

L y ( 4 ) - L y = L { δ t - 1

s 4 Y s - s 3 y 0 - s 2 y ' ' 0 - s y ' ' 0 - y ' ' ' 0 - Y s = e - s

Passo 2

Aplique as condições iniciais y 0 = 0 ,   y ' 0 = 0 ,   y ' ' ( 0 ) = 0 ,   y ' ' ' ( 0 ) = 0 .

s 4 Y s - Y s = e - s

( s 4 - 1 ) Y s = e - s

Y s = 1 s 4 - 1 e - s

Agora teremos que usar frações parciais. Sendo s 4 - 1 uma diferença de quadrados podemos escrever:

Y s = 1 s 2 - 1 s 2 + 1 e - s

Sendo s 2 - 1 também uma diferença de quadrados:

Y s = 1 s + 1 s - 1 s 2 + 1 e - s

Y s = A s + 1 + B s - 1 + C s + D s 2 + 1 e - s

Comparando:

1 s + 1 s - 1 s 2 + 1 = A s + 1 + B s - 1 + C s + D s 2 + 1

1 s + 1 s - 1 s 2 + 1 = A s - 1 s 2 + 1 s + 1 + B s + 1 s 2 + 1 s - 1 + C s + D s + 1 s - 1 s 2 + 1

1 = A s 3 - s 2 + s - 1 + B s 3 + s 2 + s + 1 + C s + D s 2 - 1

1 = A s 3 - A s 2 + A s - A + B s 3 + B s 2 + B s + B + C s 3 - C s + D s 2 - D

0 s 3 + 0 s 2 + 0 s + 1 = A + B + C s 3 + - A + B + D s 2 + A + B - C s + - A + B - D

Comparando os coeficientes:

A + B + C = 0 - A + B + D = 0 A + B - C = 0 - A + B - D = 1

Somando a segunda linha com a quarta linha multiplicada por - 1 achamos:

2 D = - 1

D = - 1 2

E o sistema fica:

A + B + C = 0 - A + B = 1 2 A + B - C = 0 - A + B = 1 2

Somando a primeira linha com terceira linha multiplicada por - 1 achamos:

2 C = 0

C = 0

E o sistema fica:

A + B = 0 - A + B = 1 2 A + B = 0 - A + B = 1 2

Somando a primeira linha com a segunda:

2 B = 1 2

B = 1 4

E logo como A + B = 0 temos que A = - 1 4 . Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):

Y s = - 1 4 ∙ 1 s + 1 + 1 4 ∙ 1 s - 1 - 1 2 ∙ 1 s 2 + 1 e - s

Y s = K s e - s

Passo 3

Agora, basta resolver esta equação e achar sua inversa. Pra isso, no entanto, precisamos saber L - 1 K s = k t , afinal:

y t = L - 1 K s e - s = k t - 1 ∙ u 1 t

Logo:

L - 1 K s = k t = L - 1 - 1 4 ∙ 1 s + 1 + 1 4 ∙ 1 s - 1 - 1 2 ∙ 1 s 2 + 1

k t = - 1 4 ∙ L - 1 1 s + 1 + 1 4 ∙ L - 1 1 s - 1 - 1 2 ∙ L - 1 1 s 2 + 1

k t = - 1 4 ∙ e - t + 1 4 ∙ e t - 1 2 ∙ sin ⁡ t

Fechamos então:

y t = - 1 4 ∙ e - t - 1 + 1 4 ∙ e t - 1 - 1 2 ∙ sin ⁡ t - 1 ∙ u 1 t

Podemos ainda ajeitar um pouco melhor, saca só:

y t = 1 2 - 1 2 ∙ e - t - 1 + 1 2 ∙ e t - 1 - sin ⁡ t - 1 ∙ u 1 t

y t = 1 2 e t - 1 - e - t - 1 2 - sin ⁡ t - 1 ∙ u 1 t

y t = 1 2 sinh ⁡ t - 1 - sin ⁡ t - 1 ∙ u 1 t

Passo 4

Abaixo está o gráfico de y ( t )   versus t .

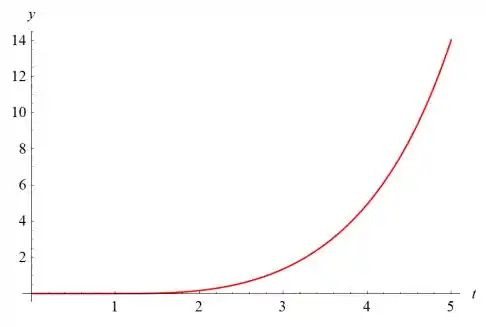
Resposta

y t = 1 2 sinh ⁡ t - 1 - sin ⁡ t - 1 ∙ u 1 t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os problemas de 17 a 22 tratam do efeito de uma sequência de impulsos aplicados em um oscilador não amortecido. Suponha que y ″+y=f( t ) ,y ( 0 )=0 ,y '( 0 )=0 . Para cada uma das escolhas para f ( t
Os problemas de 17 a 22 tratam do efeito de uma sequência de impulsos aplicados em um oscilador não amortecido. Suponha que y ″+y=f( t ) ,y ( 0 )=0 ,y '( 0 )=0 . Para cada uma das escolhas para f ( t
Considere o problema de valor inicial y ″+y=f k( t ) ,y ( 0 )=0 ,y '( 0 )=0 , em que f k ( t )=[ u 4 – k ( t )–u 4 + k ( t ) ] / 2 k com 0k≤1 .(a) Encontre a solução y=ϕ ( t ,k ) do problema de valor
Em cada um dos problemas de 11 a 23, use a transformada de Laplace para resolver o problema de valor inicial dado.13. y ' ' - 2 y ' + 2 y = 0 ; y 0 = 0 ; y ' 0 = 1
Em cada um dos problemas de 11 a 23, use a transformada de Laplace para resolver o problema de valor inicial dado.11. y ' ' - y ' - 6 y = 0 ; y 0 = 1 , y ' 0 = - 1