Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.5 - Ex. 16

Considere o problema de valor inicial

y ″   +   y   =   f k   ( t ) ,   y ( 0 )   =   0 ,   y '   ( 0 )   =   0 ,

em que f k ( t )   =   [ u 4 – k ( t )   –   u 4 + k ( t ) ] / 2 k com 0   <   k   ≤   1 .

(a) Encontre a solução y   =   ϕ ( t ,   k ) do problema de valor inicial.

(b) Calcule l i m k → 0 + ϕ ( t ,   k ) da solução encontrada no item (a).

(c) Observe que l i m k → 0 + f k ( t )   =   δ ( t   –   4 ) . Encontre a solução ϕ 0 ( t ) do problema de valor inicial

dado com f k ( t ) substituído por δ ( t   –   4 ) . É verdade que   ϕ 0 ( t ) = l i m k → 0 +   ϕ ( t ,   k ) ?

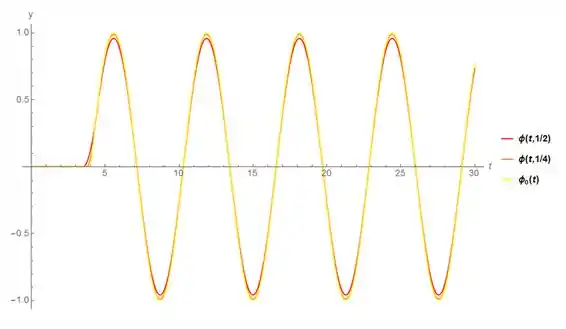
(d) Faça os gráficos de ϕ ( t ,   1 / 2 ) ,   ϕ ( t ,   1 / 4 )   e   ϕ 0 ( t ) nos mesmos eixos. Descreva a relação entre ϕ ( t ,   k ) e ϕ 0 ( t ) .

Passo 1

a)Para encontrarmos a solução y do problema de valor inicial, trabalharemos com Laplace.

Aplicando a transformada de Laplace na equação diferencial:

L y ' ' + y = L y ' ' + L y

L y ' ' + y = s 2 Y s - s y 0 - y ' 0 + Y s

L y ' ' + y = s 2 Y s + Y s

L y ' ' + y = s 2 + 1 Y s

Olhando no item 12 da tabela 6.2.1, temos que a transformada de Laplace nos da seguinte equação:

L f k t = L 1 2 k u 4 - k t - 1 2 k u 4 + k t = e - 4 - k s   2 k s - e - 4 + k s 2 k s

Igualando a primeira equação a e está equação temos:

s 2 + 1 Y s = e - 4 - k s   2 k s - e - 4 + k s 2 k s

Isolando Y s :

Y s = e - 4 - k s   2 k s s 2 + 1 - e - 4 + k s 2 k s s 2 + 1

Passo 2

Para lidarmos com Y s , trabalharemos com frações parciais:

Reescrevendo Y s com frações parciais:

1 s s 2 + 1 = A s + B s + C s 2 + 1 s s 2 + 1

1 = A s 2 + 1 + B s + C s

1 = A + B s 2 + C s + A

Equacionando os dois lados dos coeficientes, teremos:

A + B = 0

C = 0

A = 1

B = - 1

Voltando para equação inicial temos da fração parcial:

Y s = 1 s - s ( s 2 + 1   e - 4 - k s 2 k - 1 s - s s 2 + 1 e - 4 + k s 2 k  

Temos nossa equação final. Mas ainda precisamos voltar para domínio de t , portanto vamos olhar nos itens 6 e 13 da tabela 6.2.1, temos:

Y s = u 4 - k t h t - 4 - k - u 4 + k t h t - 4 + k 2 k ,   h t = 1 - cos ⁡ t

Passo 3

b)Bem no item (b) não temo muito segredo mesmo, vamos coletar a resposta do item (a) e aplicar o limite desejado:

lim k → 0 + ⁡ ϕ t , k = l i m k → 0 + u 4 - k t h t - 4 - k - u 4 + k t h t - 4 + k 2 k

= l i m k → 0 + u 4 - k t h 1 - cos ⁡ t - 4 - k - u 4 + k t h 1 - cos ⁡ t - 4 - k 2 k

Para t < 4 - k , temos que o lim k → 0 + ⁡ ϕ t , k = 0 , e teremos t > 4 + k ,

lim k → 0 + ⁡ ϕ t , k = lim k → 0 + ⁡ 1 - cos ⁡ t - 4 + k - 1 - cos ⁡ t - 4 + k 2 k

lim k → 0 + ⁡ - cos ⁡ t - 4 + k + cos ⁡ t - 4 + k 2 k

usando soma e produto e conversão trigonométrica, teremos:

lim k → 0 + ⁡ s e n   t - 4 s e n ( k ) k

= s e n   t - 4 l i m k → 0 + s e n k k

= s e n   t - 4

Nós não temos que considerar valores de t em 4 - k , 4 + k pois sempre serão aplicáveis para k ' bem pequenos, portanto t não é 4 - k ' , 4 + k ' :

l i m k → 0 + ϕ t , k = u 4 t s e n   ( t - 4 )

Passo 4

c) a função f k t é definida pelo mesmo jeito que d τ ( t - 4 )   , da pagina 344 do livro, temo que τ = k . Desde que δ t é definido até o limite de d τ ( t ) com τ → 0 + ,   temos que lim k → 0 + ⁡ f k t = l i m k → 0 + d k t - 4 = δ t - 4 .

Temos que a transformada de Laplace de δ t - 4 é e - 4 s , portanto:

Y s = e - 4 s   s 2 + 1

Aplicando a transformada inversa em Y ( s ) temos:

ϕ 0 t = y = u 4 t s e n   t - 4

Segundo nossa equação temos que ϕ 0 t = l i m k → 0 + ϕ t , k é verdade.

E por final vamos utilizar todos nosso calcular para plotar o gráfico das funções:

d)plotando ϕ t , 1 2 , ϕ t , 1 4   e   ϕ 0 t . Tendo k bem próximo de zero, tendendo o valor próximo de 1 da amplitude, temos:

Resposta

a) Y s = u 4 - k t h t - 4 - k - u 4 + k t h t - 4 + k 2 k ,   h t = 1 - cos ⁡ t

b) l i m k → 0 + ϕ t , k = u 4 t s e n   ( t - 4 )

c)

Segundo nossa equação temos que ϕ 0 t = l i m k → 0 + ϕ t , k é verdade.

d) k se aproxima de zero logo a amplitude se aproxima de 1.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + 4 y = 2 δ ( t - π / 4 ) ;y ( 0 ) = 0 ,y ' ( 0 ) = 0 .
Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + y = u π / 2 ( t ) + 3 δ ( t - 3 π / 2 ) - u 2 π ( t ) ;y ( 0 ) = 0 ,y ' ( 0 ) = 0 .
Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + 4 y = δ ( t - 4 π ) ;y ( 0 ) = 1 2 , y ' ( 0 ) = 0 .
Considere o problema de valor inicial y ' ' + γ y ' + y = δ ( t - 1 ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 , em que γ é o coeficiente de amortecimento (ou resistência).Seja γ = 1 2 . Encontre a solução do prob
Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + 3 y ' + 2 y = δ ( t - 5 ) + u 10 ( t ) ;y ( 0 ) = 0 ,y ' ( 0 ) = 1 2