Encontre a solução do problema de valor inicial dado. Depois faça um gráfico da solução...

Beleza!! Então, primeira coisa é achar a equação característica dessa equação, para encontrar nossa solução homogênea:

Como fazer isso? Bem, vamos escrever uma equação em que o grau da variável será o mesmo grau da derivada e igualar ela a 0. Vai ficar mais claro escrevendo, olha só como fica nossa equação característica:

Vamos encontrar as raízes dessa equação. Podemos colocar o em evidência:

Opa, isso nos dá que uma das raízes é 0. E as outras duas? Elas virão da equação de 2° grau do parênteses:

Tranquilo até aqui? Ok, e como fica nossa solução homogênea? Vamos com calma. Temos 3 raízes e duas são complexas. Vamos ver a raiz primeiro. Sua solução seria assim:

Beleza? A complexas são dadas por:

Opa, para chegarmos na solução homogênea completa, basta somar essas duas que achamos:

Agora, vamos para a solução particular!

Agora, para achar a solução particular, temos que olhar para a função que está à direita do igual:

Hmmm, essa função é . Então, qual seria uma boa solução particular para essa EDO? Podemos chutar uma solução . Ok? E, substituindo isso na EDO:

Assim:

Por comparação entre os dois lados da igualdade, vemos que:

E:

Opa, dessa forma, nossa solução particular será:

Agora é só juntar as souções particular e homogênea, para termos a geral:

Para achar as constantes, vamos substituir as condições iniciais:

Dessa forma, temos que:

Assim:

E:

Opa, já achamos uma constante. Mas ainda temos:

Hehehe e como já vimos ali em cima, temos que , então:

Tudo certo!! Falta só substituir os valores na solução que tínhamos, ficando com:

E fazer seu gráfico:

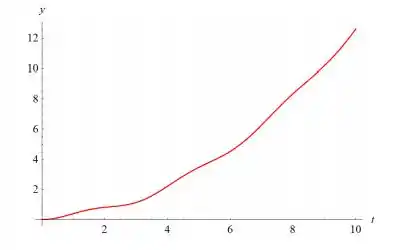
Prontinho! Acabou! 😊