Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.7 - Ex. 13
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio quando varia de
(b) Encontre a taxa de variação instantânea quando
(c) Mostre que a taxa de variação da área de um círculo em relação a seu raio (para qualquer ) é igual a circunferência do círculo. Tente explicar geometricamente por que isso é verdadeiro, desenhando um círculo cujo raio foi aumentado em . Como você pode aproximar a variação resultante em área se for pequeno?
Passo 1
Fala, galera! Beleza?
Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a taxa de variação média da área de um círculo em relação ao seu raio , quando varia em diferentes intervalos:
Depois disso, devemos encontrar a taxa de variação instantânea dessa área quando , ou seja, . E por fim, vamos mostrar que a taxa de variação da área da um círculo em relação a seu raio é igual a circunferência do círculo, para qualquer raio .
Como a gente tá falando de taxa de variação, vamos precisar usar a fórmula:
Só que no nosso caso, essa função é a área da circunferência e ela tá variando em relação ao raio . Então, teremos:
Dessa forma, basta substituir os intervalos que o enunciado nos deu, para descobrir a taxa de variação média em cada um deles. Depois, calcularemos a derivada de , no ponto , para obter . E por fim, vamos analisar o comportamento da função à medida que o raio é alterado.
Vamos lá!
Passo 2
Para resolver o item (a), vamos substituir os intervalos que o enunciado nos deu na fórmula da taxa de variação da área que vimos no passo .
Dessa forma, para de a , temos:
Como , nosso numerador fica:
E temos:
Agora para de a , temos em :
E no item , para de a , vamos ter:
Tranquilo até aqui?
Passo 3
Agora vamos calcular a taxa de variação instantânea pedida no item (b), através da derivada da função .
Assim, temos:
E para :
Show?
Passo 4
Lembra que a circunferência de um círculo é dada por
E a taxa de variação da área em relação ao raio é
Então,
Podemos demonstrar isso geometricamente da seguinte forma, veja o círculo abaixo:
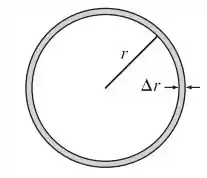
Ao calcularmos , ficamos com:
Substituindo a fórmula da área:
Expandindo o termo ao quadrado:
E simplificando, temos:
Porém, se for muito pequeno . Dessa forma, teremos:
Então,
Isso quer dizer que que a taxa de variação da área de um círculo em relação a seu raio (para qualquer ) é igual a circunferência do círculo , como queríamos demonstrar.
Valeu, galera! Até a próxima! 😉
Resposta
a)
b)
c)