Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.3 - Ex. 30
Encontre as trajetórias ortogonais da família de curvas.
Passo 1
O problema pede para achar as trajetórias ortogonais as curvas dadas. Para isso, o prosseguimento é o seguinte:
Primeiro achamos a inclinação das tangentes tomando as derivadas:
Como queremos a trajetórias ortogonais, a inclinação das curvas que procuramos é dada por
Neste caso, temos
Portanto,
Portanto,
Passo 2
Desta forma, a inclinação das trajetórias ortogonais serão
Para achar as curvas , basta fazer
Assim,
Integrando dos dois lados obtemos a equação para as trajetórias ortogonais:
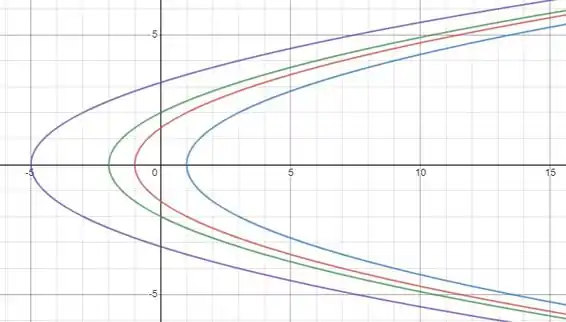
Na figura a seguir esboçamos algumas dessas curvas para diferentes valores de :
Resposta
Exercícios de Livros Relacionados
Resolva as equações diferenciais y ' + x e y = 0
Resolva as equações diferenciais e y - 1 y ' = 2 + cos x
Resolva as equações diferenciais d u d t = 1 + t 4 u t 2 + u 4 t 2
Resolva as equações diferenciais d y d x = x y
Resolva as equações diferenciais d y d x = 3 x ² y ² ² ²