Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.5 - Ex. 5

Encontre o valor médio da função no intervalo dado.

f t = t e - t ² ,           [ 0,5 ]

Passo 1

Muito bem, antes de começar vamos lembrar de como se calcula o valor médio da função, ok?

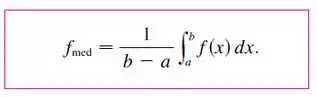
Tranquilo, não é?

Só vamos substituir:

f m e d = 1 5 - 0 ∫ 0 5 t e - t ² . d t

Para resolver usamos a substituição:

u = - t ²

Derivando:

d u = - 2 t . d t → - d u 2 = t d t

Substituindo:

f m e d = 1 5 ∫ 0 5 e u . - d u 2

A constante sai da integral:

f m e d = - 1 10 ∫ 0 5 e u . d u

f m e d = - 1 10 e u | 5 0

Substituindo u:

f m e d = - 1 10 e - t ² | 5 0

Aplicando o intervalo:

f m e d = - 1 10 e - 5 2 - e - 0

f m e d = 1 10 1 - e - 25

E prontoo!

Resposta

f m e d = 1 10 1 - e - 25

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache x 0t a lq u ef xt e n h av a l o rm é d i o ,c o mxn oi n t e r v a l o[ 3,0 ] é f x = 9 - x ² ²
Ache x0 tal que f(x) tenha valor médio, com x no intervalo [4,0] f x = 8 x - x ² ²
Determine o valor médio de ln ⁡ x em [ 1 , e ] .
É verdade que o valor médio de uma função integrável em um intervalo de comprimento 2 é a metade da integral da função ao longo do intervalo? Justifique sua resposta.
Verifique que ∫ ln ⁡ xd x = x ln ⁡ x - x + C .