Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.5 - Ex. 10
- Encontre o valor médio de no intervalo dado.
- Encontre tal que .
- Esboce o gráfico de e um retângulo cuja área seja a mesma que a área sob o gráfico de .
Passo 1
Bora fazer essa questão! O enunciado nos dá:
E a primeira coisa que ele pede é que a gente encontre o valor médio no intervalo dado. Por definição o valor médio de uma função em um certo intervalo é dado por:
Assim, podemos escrever que o valor médio para nossa função é dado por:
Resolvendo a equação anterior, temos que:
Lembre-se que :
Passo 2
Agora queremos achar tal que . Para isso podemos substituir o valor médio obtido no passo anterior na função dada, assim temos que:
Passo 3
Pra acabar a gente vai esboçar o gráfico de e um retângulo cuja área seja a mesma que a área sob o gráfico de .
Se a média é então o retângulo deve ter essa altura e o comprimento do intervalo de integração. Assim teremos:
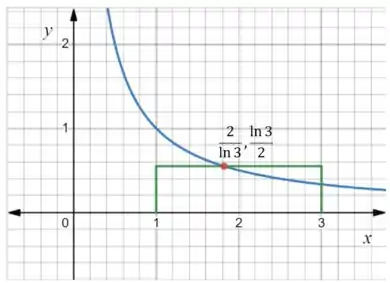
Prontinho!
Resposta
- Gráfico acima.
Exercícios de Livros Relacionados
Em uma certa cidade a temperatura (em ºC) t horas depois das 9 horas foi aproximada pela função T t = 20 + 6 . s e nπ t 12 Calcule a temperatura média durante o período entre 9 h e 21 h.
Encontre o valor médio da função no intervalo dado. f x = x 2 x 3 + 3 2 , - 1,1
Encontre o valor médio da função no intervalo dado. h u = ln u u , 1,5
Encontre o valor médio de f no dado intervalo.Encontre c cujo f m e d = f ( c ) Esboce o gráfico de f e o retângulo cuja área é a mesma da área abaixo do gráfico de f 2 x e - x 2 , 0 , 2
Encontre o valor médio da função no intervalo dado. g x = x ² 1 + x ³ ,[ 0,2 ] ² ³