Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 16
Encontre e . Para quais valores de t a curva é côncava para cima?
Passo 1
Olá, meu amigo. Vamos resolver essa atividade.
Aqui a gente precisa derivar duas vezes:
E
Para isso, a gente precisa utilizar a regra da cadeia, já que a gente está com funções parametrizadas.
Chegamos a uma parte que temos uma regra da cadeia. Para calcular a derivada vamos precisar de uma sagacidade agora. (o que eu vou te mostrar um matemático teria um ataque cardíaco, mas funciona para compreender, rsrs )
Ou podemos escrever como
Se queremos a primeira derivada de , então usamos essa formulinha. Agora, para a derivada segunda podemos fazer o seguinte:
É o mesmo conceito, só precisamos mudar um pouco a equação que estamos derivando :) Vamos calcular primeiro a primeira derivada.
Depois disso, a gente vai precisar responder para quais valores de a curva será concava para cima.
Para que nossa concavidade seja para cima a sefunda derivada precisa ser positiva
Passo 2
Temos então:
Então vamos arregaçar as mangas e cair dentro
Vamos só lembrar que
Show! Então como fica nossa derivada?
Passo 3
Agora vamos calcular a derivada segunda
Aqui a gente vai precisar aplicar a regra do quociente para derivar o numerador:
Aplicando, a gente tem:
A gente vai simplificar as frações:
Passo 4
Para que nossa concavidade seja para cima a sefunda derivada precisa ser positiva
Contudo temos nossa equação não tem resoluão. Vamos plotar o grafico dela:
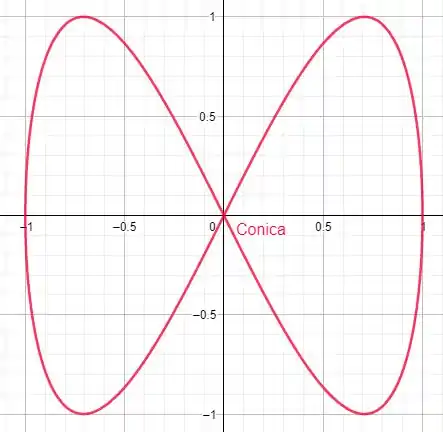
Esse formato não é bijetor, e de fato como ela é ciclica nossa resposta teria um conjunto infinito de soluções pelos loops da nossa curva. Belezinha. Terminamos por aqui, te vejo na próxima resolução. :)