Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 11
Desenhe um exemplo de uma região que seja:
- Do tipo mas não do tipo .
- Do tipo mas não do tipo .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Item a:
Para que uma região seja dita do tipo , ela deve ser uma região entre o gráfico de duas funções contínuas de . Ou seja:
Vamos ao desenho para ficar mais claro:
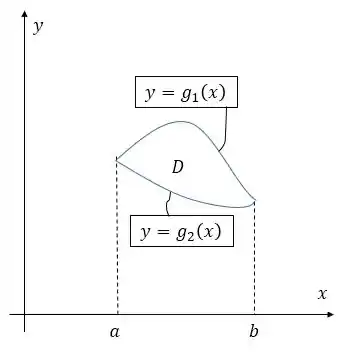
Podemos ver que a região é contínua em de para .
Passo 2
Item b:
Para que uma região seja dita do tipo , ela deve ser uma região entre o gráfico de duas funções contínuas de . Ou seja:
Vamos ao desenho para ficar mais claro:
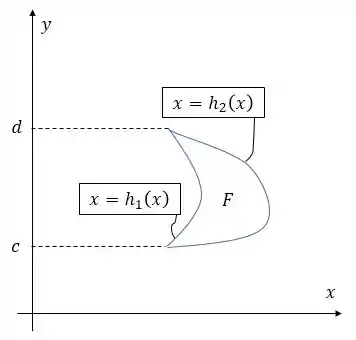
Podemos ver que a região é contínua em de para d.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
8. Calcular ∬_R^() (y l n x)/(x) d y d x , onde R é o retângulo 1 = x = 2 e - 1 = y = 1 .
12. Calcular ∬_R^() (x^2)/(y^2) d x d y onde R é a região delimitada por y = x ; y = (1)/(x) e x = 2 .
11. Calcular ∬_R^() ( 2 x + y ) d x d y onde R é a região delimitada por x = y^2 - 1 ; x = 5 ; y = - 1 e y = 2 .
5. Calcular ∬_R^() ( 8 - x - y ) d x d y , onde R é a região delimitada por y = x^2 e y = 4 .
7. Calcular ∬_R^() sen x sen y d x d y , onde R é o retângulo 0 = x = (pi)/(2) e 0 = y = (pi)/(2) .