Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.9 - Ex. 16

Determine o centro de massa do conjunto - 1 ≤ x ≤ 3 e 0 ≤ y ≤ x + 1 2 . (Sugestão: Resolva o problema no plano u , y , com u = x + 1 .)

Passo 1

Vamos fazer u = x + 1 e substituir nos intervalos:

- 1 ≤ x ≤ 3 → - 1 ≤ u - 1 ≤ 3 → 0 ≤ u ≤ 4

0 ≤ y ≤ u - 1 + 1 2 → 0 ≤ y ≤ u 2

Temos então que podemos achar os centros de massa com as fórmulas:

u c = ∫ a b u g u - f u d u á r e a   d e   A

y c = 1 2 ∫ a b g u + f u g u - f u d u á r e a   d e   A

Onde a ≤ u ≤ b e f u ≤ y ≤ g u .

Passo 2

Vamos substituir então:

u c = ∫ a b u g u - f u d u á r e a   d e   A = ∫ 0 4 u u 2 - 0 d u á r e a   d e   A = ∫ 0 4 u 3 d u á r e a   d e   A

y c = 1 2 ∫ a b g u + f u g u - f u d u á r e a   d e   A = 1 2 ∫ 0 4 u 2 + 0 u 2 - 0 d u á r e a   d e   A = 1 2 ∫ 0 4 u 4 d u á r e a   d e   A

Falta achar a área, vamos calcular!!

Passo 3

Vamos achar a área de A analisando o gráfico abaixo:

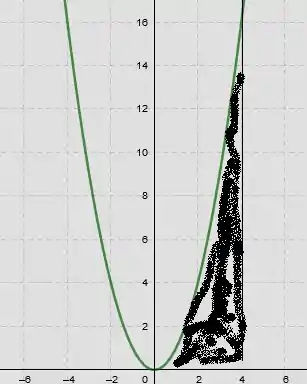
Temos que a área pode ser calculada pela integral abaixo:

A = ∫ 0 4 u 2 - 0 d u = ∫ 0 4 u 2 d u = u 3 3 0 4 = 4 3 3 = 64 3

Pronto, agora é só substituir:

u c = ∫ 0 4 u 3 d u á r e a   d e   A = u 4 4 0 4 64 3 = 4 4 4 64 3 = 256 4 ⋅ 3 64 = 3

y c = 1 2 ∫ 0 4 u 4 d u á r e a   d e   A = 1 2 u 5 5 0 4 64 3 = 1 2 4 5 5 64 3 = 1 2 4 5 5 ⋅ 3 64 = 24 5

Resposta

u c = 3

y c = 24 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Dê uma estimativa para o valor de k ( 0k1 ), tal que a região englobada por y = 1 / 1 - x 2 , y = x ,x = 0 e x = k tenha uma área de 1 unidade.
Use um recurso gráfico computacional, quando necessário, para encontrar a área da região englobada pelas curvas. x = y 3 - y , x = 0
Encontre a área da região englobada pela parábola y = 2 x - x 2 e o eixo x .Encontre o valor de m de tal forma que a reta y = m x divida a região de (a) em duas regiões de mesma área.