- Se , encontre .
- Verifique se sua resposta em (a) é razoável, comparando os gráficos de e .
Passo 1
Oi galerinha, bora resolver mais uma comigo?
Claro! Vamos lá.
Para encontrar a derivada de , primeiro aplicamos a regra do produto, que afirma que a derivada de uma função do produto é dada pela derivada da primeira função vezes a segunda função mais a primeira função vezes a derivada da segunda função.
Então, aplicando esta regra, temos:
Agora, precisamos calcular as derivadas das duas partes.
1. Derivada de usando a regra de potência:
2. Derivada de que é a própria função exponencial:
Substituindo esses valores na expressão de temos:
Essa é a derivada de que é
Agora, para verificar se a resposta é razoável, podemos comparar os gráficos de e . Se representa a taxa de variação de então os pontos críticos de (onde ou não está definida) indicarão pontos importantes no gráfico de
Passo 2
Desenhando o gráfico,
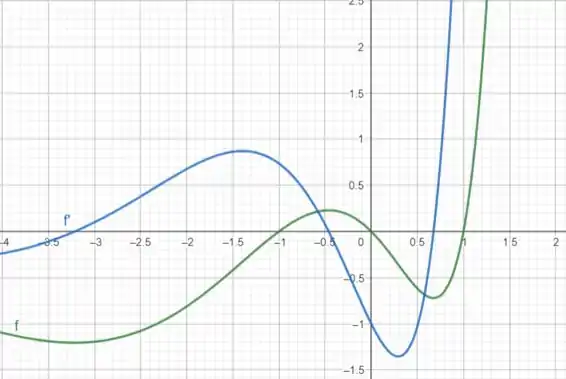
A derivada nos mostra a inclinação da reta tangente ao gráfico da função. Então, pelo gráfico, quando a derivada é positiva, a reta tangente tem inclinação crescente e, consequentemente, a função também cresce. O oposto também acontece. E quando a derivada é zero, a reta tangente tem uma inclinação horizontal,