Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.6 - Ex. 52
51 – 52 Encontre . Verifique se sua resposta é razoável comparando os gráficos de e .
52.
Passo 1
Fala aí, tudo certinho com você?
Essa questão pede pra gente encontrar a derivada da função
E depois verificar se nossa resposta é razoável comparando os gráficos de e .
Então a ideia aqui é ver direitinho qual é o tipo de função que estamos derivando para determinar a regra de derivação mais adequada.
E perceba que nossa função é formada por uma multiplicação entre duas outras funções
Veja:
Podemos pensar nela da seguinte forma:
Onde
E
Sendo assim, a regra mais adequada para derivr essa função é a regra do produto.
Ela é a seguinte:
Então, já sabemos por onde começar. Vem comigo que te mostro tudinho no passo a passo.
Passo 2
Nossa função é:
E estamos pensando nela da seguinte forma:
Assim, sua derivada sera:
Então precisaremos das funções , e de suas derivadas. Então, teremos:
E
Já
Para derivarmos precisamos utilizar a regra da cadeia, pois temos uma função dentro da outra.
Essa regra diz que quando temos uma “função dentro da outra”, do tipo
e queremos derivá-la, a gente faz a derivada da função de fora e multiplica pela derivada da função de dentro:
Nesse caso a função de fora é o arco seno e a função de dentro é , então podemos escrever a equação como sendo:
A derivada do arco seno é tabelada e dada por:
Assim:
Agora que já temos tudo que precisávamos, basta substituir.
Passo 3
E sendo
e
E substituindo, ficamos com:
Então a derivada da função fica:
Multiplicando ficamos com:
E ajeitando um pouco mais, teremos:
Prontinho, derivada calculada.
Passo 4
Para comparar os gráficos precisamos plotá-los com o auxilio de algum software, eu vou usar o GeoGebra que é online e fácil de usar, só escrever a função que aparece lá:
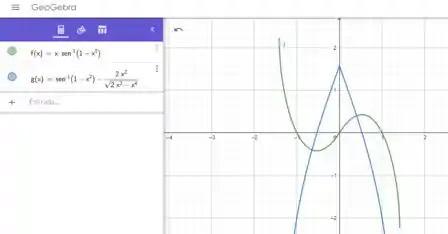
A função verde é a que tínhamos no começo e a azul é sua derivada calculada por nós.
A função calculada por nós faz sentido:
Na coordenada em que a função atinge seu mínimo e seu máximo a derivada cruza o zero.
Onde a função está decrescendo a derivada realmente está negativa e onde a função está crescente a derivada está positiva.