Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.6 - Ex. 51
Encontre . Verifique se sua resposta é razoável comparando os gráficos de e .
Passo 1
Fala aí, galerinha!
Nesse problema queremos encontrar a derivada da função
E tambem camparar os gráficos de e .
Parece complicado?
A primeira coisa que podemos observar dessa função é que em um termo temos um produto de funções, no caso, em .
Então quando formos derivar esse termo, vamos ter que aplicar a regra do produto...
A regra do produto é dada por
Sacou? Bora começar!
Passo 2
Vamos começar derivando a função inteira
Como a derivada da soma é igual a soma das derivadas
Na derivada de aplicamos a regra do produto
Agora é só aplicar o teorema fundamental do calculo, onde
Substituindo em
Tranquilo até aqui?
Passo 3
Para comparar os gráficos precisamos plota-los com o auxilio de algum software, eu vou usar o GeoGebra que é online e fácil de usar, só escrever a função que aparece lá:
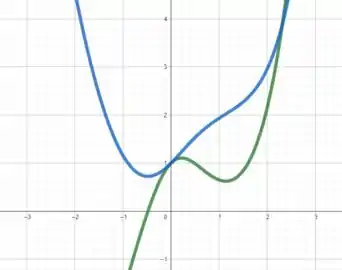
A função azul é a que tínhamos no começo e a verde é sua derivada calculada por nós.
A função calculada por nós faz sentido:
- Na coordenada em que a função atinge seu mínimo a derivada cruza o zero.
- Onde a função está decrescendo a derivada realmente está negativa e onde a função está crescente a derivada está positiva.
- Vemos dois pontos de inflexão na função original e nas coordenadas desses ponto a função da derivada atinge seus máximos e mínimos locais.
É isso! O que achou? Responde Aí!