Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 74
As curvas de nível são mostradas para uma função . Determine se as seguintes derivadas parciais são positivas ou negativas no ponto .
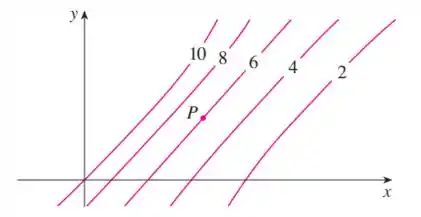
(a) (b) (c) (d) (e)
Passo 1
Opa, tudo bom? Questãozinha de derivadas parciais com um gráfico de curvas de nível, vamos lá!
Nessa questão nós temos um mapa de contorno de uma função e temos que determinar se as derivadas parciais são positivas ou negativas.
Para uma função normal a gente fixaria uma variável e verificaríamos a variação do valor de conforme a outra variável muda. Mas e no nosso caso, onde só temos um gráfico de contorno?
Não tem problema, como só precisamos dizer se a derivada é positiva/negativa o valor das curvas de nível é suficiente.
Da mesma forma para as variáveis de segunda ordem: A diferença é que para isso analisamos a variação na derivada de primeira ordem!
Passo 2
(a)
Queremos saber o sinal de no ponto , para isso fixamos o valor de no ponto e verificamos a variação de com o aumento de .
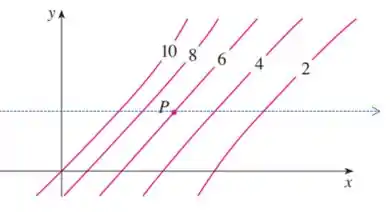
Em outras palavras: Traçamos uma reta onde o valor de está fixo no ponto e observamos: O que acontece com o valor da função (o valor das curvas de nível) conforme aumenta?
No ponto estamos na curva de nível onde e, ao aumentarmos o valor de , seguimos em direção ao valor de Isso indica que a função está decrescendo. Logo, negativo.
Passo 3
(b)
De forma similar, queremos saber o sinal de no ponto , para isso fixamos o valor de no ponto e verificamos a variação de com o aumento de .
Nota-se que o ponto P está na curva de nível e, ao aumentarmos o valor de , seguimos em direção ao valor de Isso indica que a função está crescendo. Logo, positivo.
Passo 4
(c)
No mesmo estilo, agora queremos saber o sinal de no ponto , para isso fixamos o valor de no ponto e verificamos a variação de com o aumento de . Mas como fazemos isso?
Pelo mapa de contorno (com o valor de fixo) nós vemos que o espaço entre as curvas de nível aumenta com o aumento do valor de , e o que isso significa?
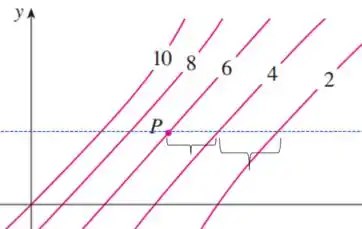
Significa que decresce com o aumento de , MAS ele decresce mais devagar (ainda é negativo, mas é um número com módulo menor). Dessa forma temos positivo.
Passo 5
(d)
No mesmo estilo, agora queremos saber o sinal de no ponto , para isso fixamos o valor de no ponto e verificamos a variação de com o aumento de . Mas como fazemos isso?
O processo é similar ao caso , mas agora observamos o comportamento da função conforme cresce, e, pelo mapa de contorno, vemos que cresce mais rapidamente no sentido positivo de (lembrando que nós percebemos isso pois o espaço entre as curvas de nível diminui, significando que aumenta mais rápido).
Como seguimos esse sentido, o valor negativo de decresce ainda mais. Logo, negativo.
Passo 6
(e)
E por último, mas não menos importante, agora queremos saber o sinal de no ponto , para isso fixamos o valor de no ponto e verificamos a variação de com o aumento de .
Seguindo com a variável fixa no ponto , nós vemos que a taxa de variação de aumenta no sentido positivo do eixo . Assim, é positivo.
Resposta
(a) Negativo
(b) Positivo
(c) Positivo
(d) Negativo
(e) Positivo