Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.3 - Ex. 30
Use camadas cilíndricas para encontrar o volume do sólido que é gerado quando a região envolvida por , gira em torno da reta .
Passo 1
Vamos começar esboçando essa região:
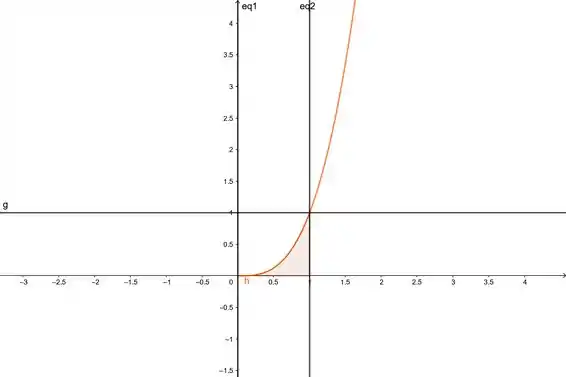
Passo 2
Nesses casos a gente tem que colocar as funções em .
O raio do cilindro quando ele rotacionar em torno de vai ser e altura vai ser ou no caso.
O intervalo a gente vai olhar em também, que vai ser .
Montamos a integral...
Resolvendo...
E prontinho! Calculamos o volume pelo método das cascas cilíndricas😉
Resposta
Exercícios de Livros Relacionados
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . y 2 = x , y = 1 , x = 0
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . y = x 2 , x = 1 , y = 0
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . x y = 4 , x + y = 5
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo x . x = 2 y , y = 2 , y = 3 , x = 0