Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 56
Encontre o volume do sólido descrito. A base de é a região triangular com vértices e . As secções transversais perpendiculares ao eixo são triângulos equiláteros.
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que encontrar o volume do solido onde a base de é a região triangular com vértices e . As secções transversais perpendiculares ao eixo são triângulos equiláteros
Pensando no enunciado temos a seguinte figura:
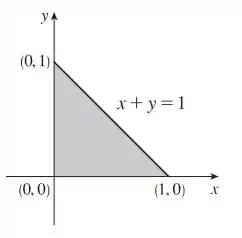
Veja só!
Passo 2
A seção transversal da base corresponde à coordenada que tem comprimento . O triângulo equilátero correspondente com lado tem área
Assim sendo, nosso volume é:
Calculando a integral e aplicando os limites de integração...
E fim! Entendeu tudo? Responde Aí!
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Encontre o volume do sólido S descrito.A base de S é um disco circular de raio r . Secções transversais paralelas, perpendiculares à base, são quadradas.
Escreva uma integral para um toro sólido (o sólido com formato de rosquinha da figura) com raios r e R .Interpretando a integral como uma área, encontre o volume do toro.
Ache o volume comum aos dois cilindros circulares, cada qual com raio r , se os eixos dos cilindros se interceptam em ângulos retos.
Um buraco de raio r é perfurado pelo centro de uma esfera de raio Rr . Encontre o volume da porção remanescente da esfera.