Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.2 - Ex. 34
Encontre o volume do sólido gerado quando a região delimitada por , e gira em torno do eixo . [Sugestão: Divida o sólido em duas partes.]
Passo 1
Bom galera, vamos começar observando o gráfico das nossas funções:
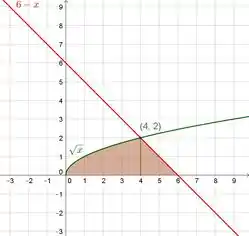
Assim, temos que no intervalo , nós somos delimitados à esquerda por , e à direita pelo eixo . E no intervalo de nós somos delimitados por na esquerda e pelo eixo na direita.
Passo 2
Belezinha, então o volume é a soma de duas integrais:
Passo 3
Por fim, resolvemos as integrais e calculamos o resultado:
Resposta
Exercícios de Livros Relacionados
Seja R a região englobada pelas curvas y = x 2 + 4 , y = x 3 e o eixo y . Encontre e calcule uma integral definida que represente o volume do sólido obtido quando R gira em torno do eixo x .
Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.