Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.Revisão - Ex. 9
Seja R a região englobada pelas curvas , e o eixo . Encontre e calcule uma integral definida que represente o volume do sólido obtido quando gira em torno do eixo .
Passo 1
Representando graficamente o espaço que as funções representam, temos:
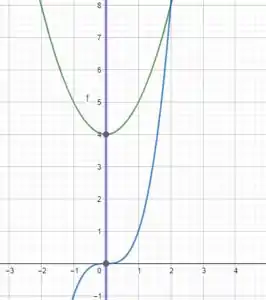
Portanto, para calcular esse volume encontramos o intervalo em relação a , assim,temos .
Passo 2
Montamos a nossa integral como resposta:
Resolvendo essa integral:
Prontinho!!!
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo y . y = 1 - x 2 x 2( x0 ) ; x = 0 ; y = 0 ; y = 2
Encontre o volume do sólido gerado quando a região delimitada por y = x + 1 , y = 2 x e y = 0 gira em torno do eixo x . [Sugestão: Divida o sólido em duas partes.]
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Nestes exercícios, suponha que um sólido S de volume V seja delimitado por dois planos paralelos perpendiculares ao eixo x
Considere o sólido que resulta quando a região sombreada do Exercício 1 gira em torno da reta y = 2 . ( a ) Faça uma conjectura sobre qual é maior: o volume desse sólido ou o volume do sólido do Exerc
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Nestes exercícios, suponha que um sólido S de volume V seja delimitado por dois planos paralelos perpendiculares ao eixo x