Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 12

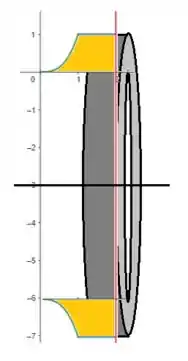
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos.

em torno de

Passo 1

Falaeee, belezinha??? Bom... a questão nos pede para calcular o volume do sólido delimitado pelas seguintes curvas:

Dado que o sólido está em torno de .

Lembrando que para um sólido que está entre e e possui área de seção transversal igual a , seu volume é dado por:

Agora vamos aplicar!! 😉

Passo 2

Dadas a equações mencionadas no enunciado temos a seguinte região que será girada é a seguinte:

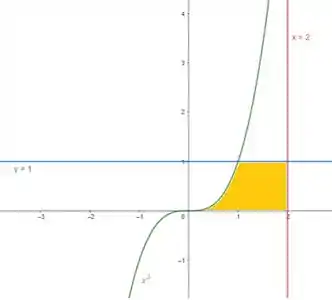
Dessa forma nossa área terá 2 raios dados por: e ,e será dada por

Assim, nosso volume é dado integrando essa região, então, teremos

Assim, temos o seguinte sólido de revolução:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7. Ache do volume do sólido gerado pela rotação em torno do eixo y da região limitada pela parábola x = y 2 + 2 e pela reta x = y + 8 .

7 - Determine o volume do sólido gerado pela rotação da região limitada pelo eixo x, pela curva y = 3 x 4 e pelas retas x = 1 e x = - 1 em torno:A - do eixo x;

7 - Determine o volume do sólido gerado pela rotação da região limitada pelo eixo x, pela curva y = 3 x 4 e pelas retas x = 1 e x = - 1 em torno:B - do reta y = 3;

7 - Determine o volume do sólido gerado pela rotação da região limitada pelo eixo x, pela curva y = 3 x 4 e pelas retas x = 1 e x = - 1 em torno:B - do eixo y;O limite de integração para este método s

7 - Determine o volume do sólido gerado pela rotação da região limitada pelo eixo x, pela curva y = 3 x 4 e pelas retas x = 1 e x = - 1 em torno:B - do reta x = 1;