Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.2 - Ex. 1
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Temos aqui uma situação onde uma região plana irá rotacionar em relação a um eixo, gerando uma região tridimensional.
Para , teremos uma curva com parábola para cima devido ao sinal positivo do coeficiente angular, como , então
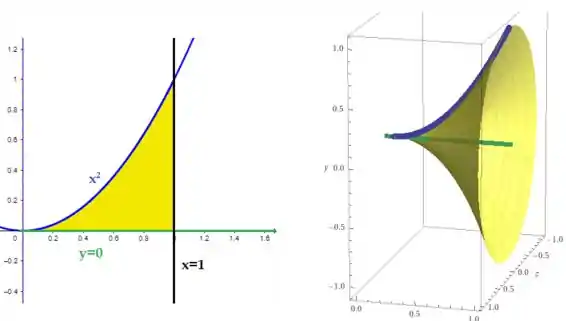
O intervalo de interseção é de (0,1). A área é
Podemos calcular o volume!!
Passo 2
Agora é só calcularmos a integral:
Sendo uma integral polinomial:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 + sec x ,y = 3 ;
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = 1 4 x 2 , x = 2 ,y = 0 ; e mt
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 1e mt o r n od eB C
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = x - 2 4 ,8 x - y = 16 ; e mt o r n od oe i x
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = c o sx ,y = 2 - cos x ,0 ≤ x ≤ 2 π ; e mt