Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.2 - Ex. 45
A ponta cônica de reentrada de um veículo espacial é desenhada de tal forma que uma seção transversal tomada pés da ponta e perpendicular ao eixo de simetria é um círculo com raio de pés. Encontre o volume da ponta cônica sabendo que seu comprimento é de 20 pés.
Passo 1
Bom galera, nosso volume é dado pela rotação da região secção da função em torno de :
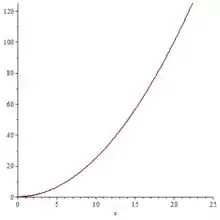
E nossa região é:
Passo 2
Belezinha, a nossa integral para o volume é:
Passo 3
Por fim, resolvemos a integral:
Resposta
Exercícios de Livros Relacionados
Sabemos do exemplo 1 que a região R = x , y x ≥ 1 ,0 ≤ y ≤ 1 / x } tem área infinita. Mostre que pela rotação de R em torno do eixo x obtemos um sólido com volume finito.
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 1 ≤ x ≤ 2 e 0 ≤ y ≤ x 3 - 1
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 1 ≤ x ≤ 4 e 1 ≤ y ≤ x
Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Encontre o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.