Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 51

A maioria das calculadoras científicas tem teclas somente para os valores de arc sen ⁡ x ,   arc cos ⁡ x e arc tg ⁡ x . As fórmulas no Exercício 50 mostram como uma calculadora pode ser usada para obter os valores de arc cotg ⁡ x , arc sec ⁡ x e arc cossec ⁡ x com valores positivos de x . Use essas fórmulas e uma calculadora para encontrar os valores numéricos para cada uma das funções trigonométricas inversas seguintes. Expresse suas respostas em graus, arredondados para o décimo de grau mais próximo.

  1. arc cotg ⁡ 0,7
  2. arc sec ⁡ 1,2
  3. arc cossec ⁡ 2,3

Passo 1

Eai galera, tranquilo? Só pra começar, como a questão fala das fórmulas do exercício anterior serem usadas pra responder as desse, vou trazer de volta elas:

  1. arc cotg ⁡ x = arc tg ⁡ 1 x ,             s e   x > 0 π + arc tg ⁡ 1 x ,           s e   x < 0
  2. arc sec ⁡ x = arc cos ⁡ 1 x ,               s e   x ≥ 1
  3. arc cossec ⁡ x = arc sen ⁡ 1 x ,               s e   x ≥ 1

E o enunciado pede:

  1. arc cotg ⁡ 0,7
  2. arc sec ⁡ 1,2
  3. arc cossec ⁡ 2,3

Em cada um desses casos, vou usar uma ferramenta famosa de planilhas pra calcular, ok? Mas você pode fazer com a sua calculadora favorita também! Para cada uma das letras, podemos usar as funções:

  1. “=ATAN()”
  2. “=ACOS()”
  3. “=ASEN()”

Pra calcular os valores desses arcos, só que em radianos. Convertemos pra graus usando a função “=GRAUS()” e arredondando já pro décimo de grau mais próximo, encontramos os seguintes valores:

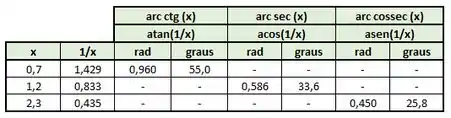
Sendo assim, ta na mão as respostas:

  1. arc cotg ⁡ 0,7 = 55,0 o
  2. arc sec ⁡ 1,2 = 33,6 o
  3. arc cossec ⁡ 2,3 = 25,8 o

Resposta

  1. arc cotg ⁡ 0,7 = 55,0 o
  2. arc sec ⁡ 1,2 = 33,6 o
  3. arc cossec ⁡ 2,3 = 25,8 o
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Enfocando conceitosSejam: f x = x 2 , x1 g x = x Mostre que f g x = x , x1 e g f x = x , x1 Mostre que f e g não são inversas uma da outra provando que os gráficos dessas funções não são reflexões um
Seja f x = a x 2 + b x + c , com a0 . Encontre f - 1 se o domínio de f for restrito a a )x ≥ - b 2 a b )x ≤ - b 2 a
Verdadeiro/FalsoDetermine se a afirmação dada é verdadeira ou falsa. Explique sua resposta31) Se f for uma função invertível tal que f 2 = 2 , então f - 1 2 = 1 2 .
Verdadeiro/FalsoDetermine se a afirmação dada é verdadeira ou falsa. Explique sua resposta32) Se f e g forem funções inversas, então f e g têm o mesmo domínio.
Prove que, se a 2 + b c ≠ 0 , então o gráfico de: f x = a x + b c x - a É simétrico em relação à reta y = x .