Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 50
A equação de movimento de uma partícula é , em que está em metros e t, em segundos.
(a) Encontre a velocidade e a aceleração como funções de t.
(b) Encontre a aceleração depois de 1 s.
(c) Trace o gráfico das funções de posição, velocidade e aceleração na mesma tela.
Passo 1
Opa! Vamos fazer essa questão! O enunciado nos dá a equação de movimento de uma partícula em função do tempo:
Com está em metros e t, em segundos e nos pede:
- As equações da velocidade e aceleração em função do tempo, e ;
- A aceleração depois de 1 segundo, ;
- As curvas de e .
Antes de qualquer coisa, vamos conversar um pouquinho! Sabemos que a velocidade é a variação do espaço percorrido pelo tempo. Então para um tempo beeem pequeninho, tendendo a zero temos:
Seguindo o mesmo raciocínio, temos que a aceleração é a variação da velocidade pelo tempo, portanto:
Precisamos então, para a letra (a), calcular a primeira e a segunda derivada de , para a letra a gente só precisa pegar a função de e calcular e finalmente na letra é só correr pro abraço plotando os gráficos!
Passo 2
Vamos calcular as derivadas:
Temos uma função polinomial, então vamos usar a regra da potência que é:
Então:
Então a velocidade em função de é dada por:
Derivando de novo:
Chegamos na a aceleração em função de :
Passo 3
Pra achar a aceleração depois de 1 segundo, é só substituir na fórmula de :
Passo 4
Pra fechar, vamos aos gráficos de:
Plotando temos:
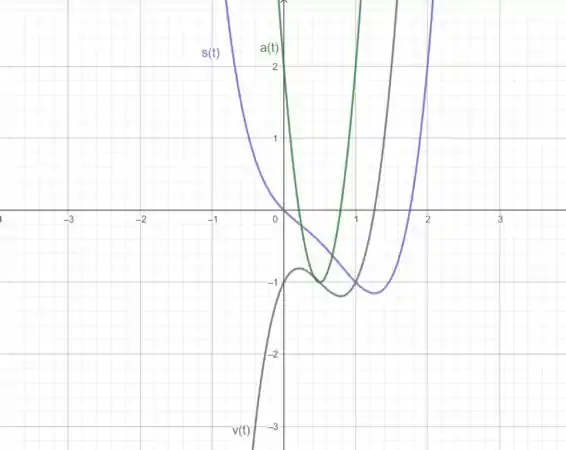
Resposta
- Esboço do gráfico.