Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.1 - Ex. 71

As Equações 4 e 5 dão fórmulas diferentes para a integral de cos - 1 ⁡ x

71 –

∫ cos - 1 ⁡ x   d x = x cos - 1 ⁡ x - s e n ( cos - 1 ⁡ x ) + c

∫ cos - 1 ⁡ x   d x = x c o s - 1 x - 1 - x 2 + c

As duas integrações podem estar corretas? Explique.

Passo 1

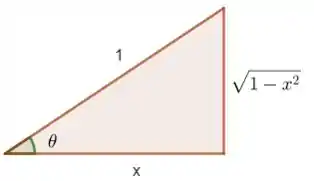
s e n ( cos - 1 ⁡ x ) , implicará para 1 - x 2 . Podemos provar esta demonstração através do triênagulo retângulo, veja:

Observe que o ângulo θ está sendo formado sobre o cateto adjacente e a hipotenusa, de acordo com as fórmula trigonométricas, temos que:

cos ⁡ θ = C a t e t o   A d j a c e n t e H i p o t e n u s a = cos ⁡ θ = x 1   : cos ⁡ θ = x

Logo o valor de θ será θ = arccos ⁡ x

Agora se observarmos:

1 - x 2 está ocupado o cateto oposto, assim utilizaremos a fórmula seno, observe: s e n   θ = 1 - x 2 1   :   s e n   θ =   1 - x 2

Como determinamos θ = arccos ⁡ x

Logo:

s e n arccos ⁡ x =   1 - x 2

Outra forma se representar a r c c o s   x é utilizar a notação: cos - 1 ⁡ x .

Fica demonstrado assim que os dois resultados são iguais.

Resposta

Sim

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral indefinida: ∫ x 2 sen ⁡ 3 x d x
Use a fórmula: ∫ f - 1 x d x = x f - 1 x - ∫ f y d y , sendo y = f - 1 ( x ) Expresse suas respostas em termos de x:69 - ∫ sec - 1 ⁡ x d x
Use a integração por partes para estabelecer a fórmula de redução:64 - ∫ ( ln ⁡ x ) n d x = x ( ln ⁡ x ) n - n ∫ ln ⁡ x n - 1
As Equações 4 e 5 dão fórmulas diferentes para a integral de cos - 1 ⁡ x 72 – ∫ tg - 1 ⁡ xd x = x t g - 1 x - ln ⁡ sec ⁡ t g - 1 x + c ∫ tg - 1 ⁡ xd x = x t g - 1 x - l n 1 + x 2 + c As duas integraçõ
Use a fórmula: ∫ f - 1 x d x = x f - 1 x - ∫ f y d y , sendo y = f - 1 ( x ) Expresse suas respostas em termos de x:68 - ∫ t g - 1 xd x