Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 11
As equações diferenciais autônomas representam modelos de crescimento populacional. Use a análise da reta de fase para esboçar curvas integrais , selecionando diferentes valores iniciais . Quais equilíbrios são estáveis e quais são instáveis?
Passo 1
A questão nos pergunta sobre os pontos de equilíbrio e, para isso, precisamos primeiramente definir como buscar um ponto de equilíbrio e como saber se ele é estável ou instável, assim, temos a seguinte definição: “Dada uma equação diferencial que dependa apenas de uma variável (normalmente os pontos para os quais são chamados de pontos de equilíbrio ou estacionários”. Além disso, esse ponto pode ser estável ou instável e isso a gente avalia através dos pontos marcados da reta de fase, se antes e depois de um número marcado na reta de fase a tendência for que os valores se aproximem dele esse ponto é dito estável, caso contrário é instável.
Passo 2
Sendo assim, vamos encontrar os pontos de equilíbrio fazendo
Encontrando a segunda derivada
De posse de todos esses pontos podemos desenhar a reta de fase marcando os pontos de equilíbrio e depois poderemos marcar os pontos os a primeira derivada é maior e menor do que 0, além disso, temos de marcar na reta os pontos onde a segunda derivada é maior e menor do que 0. Assim poderemos marcar as tendências em relação aos pontos de equilíbrio
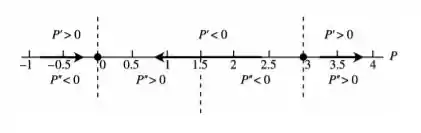
Dessa forma, podemos inferir que e ponto de equilíbrio estável e é ponto de equilíbrio instável.
Passo 3
Agora que fizemos a reta de fase podemos desenhar retas horizontais nos pontos de equilíbrio e desenhar as curvas integrais de acordo com as tendências apresentadas na reta, portanto, teremos
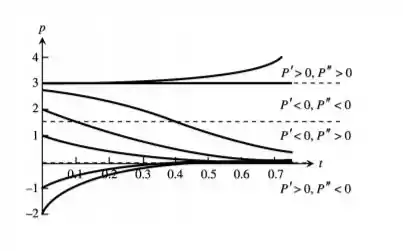
Resposta
Ei, a resposta está no passo a passo :)