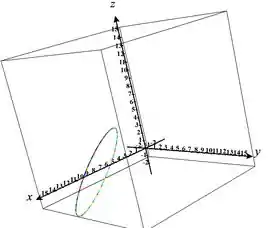
Esboçar a trajetória de uma partícula , sabendo que seu movimento é descrito por:
(h)
Passo 1
Pessoal, vamos abrir essa função de movimento nas componentes , e :
Vamos fazer uma manipulação algébrica aqui. A parametrização de uma elipse é dada por:
Na nossa questão já temos os valores de e nesse formato! Logo, sabemos já o valor de e .
Assim, podemos escrever a equação da elipse como:
Portanto, nossa trajetória é elíptica, no plano .
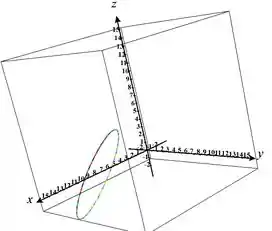
Resposta
A trajetória é igual a: