Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 6
Esboce a área apresentada por . A seguir, encontre
- Utilizando a parte 1 do teorema fundamental do cálculo parte 1
- Calculando a integral usando a parte 2, e então, derivando.
Passo 1
Bom pessoal, nessa questão nós temos a função
Primeiro temos que esboçar a área representada por essa função. Para isso, basta fazer o gráfico da função , transladada em 2 unidades para cima.
Depois teremos que encontrar a derivada de , isso é,
Na letra a), vamos usar a parte 1 do teorema fundamental do cálculo que diz que se temos uma função:
Então, teremos:
Já na letra b), teremos que encontrar essa mesma derivada mas para isso vamos calcular o valor da integral e então derivar.A resposta tanto na a) quanto na b) devem dar o mesmo resultado!
Passo 2
Sabendo que a área da função é o “espaço “entre o gráfico da função e a curva. Vamos esboçar!
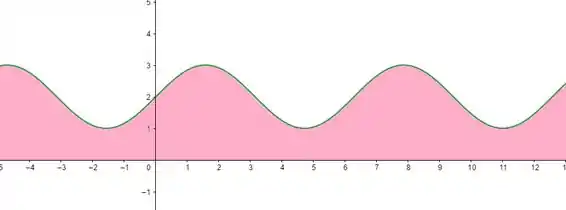
Esbocei aí o gráfico da função , só que transladado em unidades para cima.
Dessa forma, ao invés de oscilar entre e , essa função oscila entre e .
Passo 3
Agora vamos resolver a letra a)
Usando o teorema fundamental do cálculo,
Então,
No nosso caso,
Então,
Simples assim!
Passo 4
Resolvendo item b), vamos calcular essa integral!
Usando a regra da soma,
O primeiro termo é resolvido com a integral da constante:
E o segundo termo é a integral do seno:
Portanto, teremos:
Ou seja,
Derivando,
Resposta
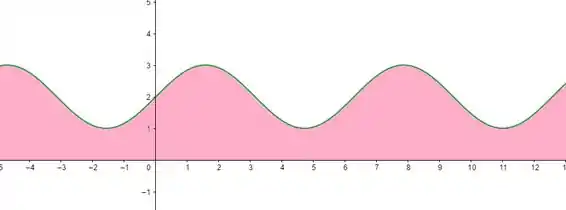
Letra a)
Letra b)