Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.2 - Ex. 9
Esboce o campo de direções para a equação diferencial. Use-o para esboçar três curvas solução.
Passo 1
Nessa questão, queremos esboçar o campo de direções para a equação . Esta equação nos diz que a inclinação em qualquer ponto no gráfico é igual a soma da sua coordenada mais uma unidade.
Então para conseguirmos fazer esse desenho, precisamos pegar vários pontos e desenhar pequenos segmentos de reta com inclinação .
Note que em temos , ou seja uma reta horizontal no gráfico. Para esboçar três curvas vamos escolher três pontos e traçar uma curva seguindo a direção do campo de direções, vamos escolher os pontos . Então, nosso desenho fica assim:
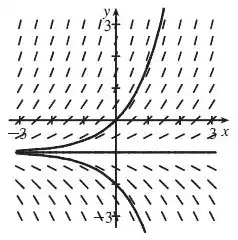
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Ligue a equação diferencial a seu campo de direções (I-IV). Dê razões para sua resposta. y ' = y - x
Ligue a equação diferencial a seu campo de direções (I-IV). Dê razões para sua resposta. y ' = y - 1
Use o campo de direções I para esboçoar os gráficos das soluções que satisfazem as condições iniciais dadas.a) y 0 = 1 b) y 0 = 0 c) y 0 = - 1
Ligue a equação diferencial a seu campo de direções (I-IV). Dê razões para sua resposta. y ' = y 2 - x 2
Ligue a equação diferencial a seu campo de direções (I-IV). Dê razões para sua resposta. y ' = y 3 - x 3